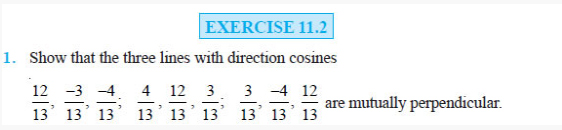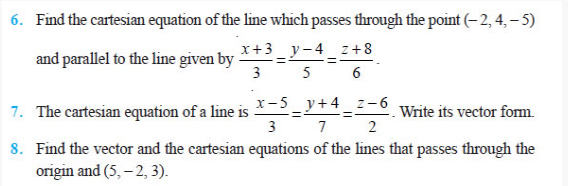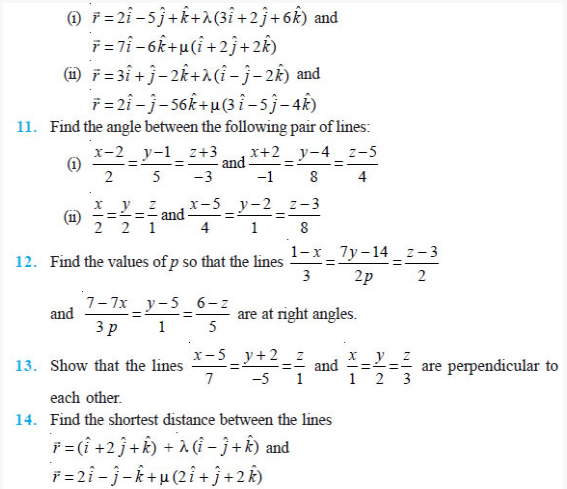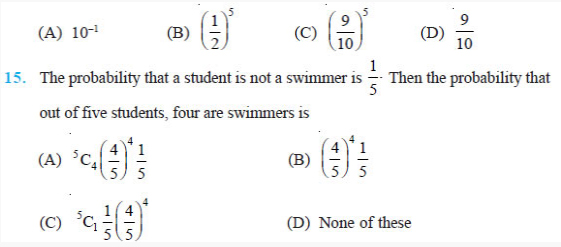![]()
NCERT Physics Question Paper (Class - 12)
:: Chapter 1 - Electric Charges And Fields ::
List of Physics Formula
![]()
![]()
![]()
![]()
EXERCISE
Question 1: What is the force between two small charged
spheres having charges of 2 × 10−7 C and 3 × 10−7 C placed 30 cm apart in air?
Question 2: The electrostatic force on a small sphere of
charge 0.4 µC due to another small sphere of charge − 0.8 µC in air is 0.2 N.
(a) What is the distance between the two spheres? (b) What is the force on the
second sphere due to the first?
Question 3: Check that the ratio ke2/G memp is dimensionless.
Look up a Table of physical constants and determine the value of this ratio.
What does the ratio signify?
Question 4: (a) Explain the meaning of the statement
‘electric charge of a body is quantised’.
(b) Why can one ignore quantisation of electric charge when dealing with
macroscopic i.e., large scale charges?
Question 5: When a glass rod is rubbed with a silk cloth,
charges appear on both. A similar phenomenon is observed with many other pairs
of bodies. Explain how this observation is consistent with the law of
conservation of charge.
Question 6: Four point charges qA = 2 µC, qB = −5 µC, qC = 2
µC, and qD = −5 µC are located at the corners of a square ABCD of side 10 cm.
What is the force on a charge of 1 µC placed at the centre of the square
Question 7: (a) An electrostatic field line is a continuous
curve. That is, a field line cannot have sudden breaks. Why not? (b) Explain why
two field lines never cross each other at any point?
Question 8: Two point charges qA = 3 µC and qB = −3 µC are
located 20 cm apart in vacuum. (i) What is the electric field at the midpoint O
of the line AB joining the two charges? (ii) If a negative test charge of
magnitude 1.5 × 10−9 C is placed at this point, what is the force experienced by
the test charge?
Question 9: A system has two charges qA = 2.5 × 10−7 C and qB
= −2.5 × 10−7 C located at points A: (0, 0, − 15 cm) and B: (0, 0, + 15 cm),
respectively. What are the total charge and electric dipole moment of the
system?
:: Chapter 2 - Electrostatic Potential and Capacitance ::
EXERCISE
Question 2.1 Two charges 5 × 10–8 C and –3 × 10–8 C are
located 16 cm apart. At what point (s) on the line joining the two charges is
the electric potential zero? Take the potential at infinity to be zero.
Question 2.2 A regular hexagon of side 10 cm has a charge 5
μC at each of its vertices. Calculate the potential at the centre of the
hexagon.
Question 2.3 Two charges 2 μC and –2 μC are placed at
points A and B 6 cm apart.
(a) Identify an equipotential surface of the system.
(b) What is the direction of the electric field at every point on this surface?
Question 2.4 A spherical conductor of radius 12 cm has a
charge of 1.6 × 10–7C distributed uniformly on its surface. What is the electric
field
(a) inside the sphere
(b) just outside the sphere
(c) at a point 18 cm from the centre of the sphere?
Question 2.5 A parallel plate capacitor with air between the
plates has a capacitance of 8 pF (1pF = 10–12 F). What will be the capacitance
if the distance between the plates is reduced by half, and the space between
them is filled with a substance of dielectric constant 6?
Question 2.6 Three capacitors each of capacitance 9 pF are
connected in series.
(a) What is the total capacitance of the combination?
(b) What is the potential difference across each capacitor if the combination is
connected to a 120 V supply?
Question 2.7 Three capacitors of capacitances 2 pF, 3 pF
and 4 pF are connected in parallel.
(a) What is the total capacitance of the combination? (b) Determine the
charge on each capacitor if the combination is connected to a 100 V supply.
Question 2.8 In a parallel plate capacitor with air between
the plates, each plate has an area of 6 × 10–3 m2 and the distance between the
plates is 3 mm. Calculate the capacitance of the capacitor. If this capacitor is
connected to a 100 V supply, what is the charge on each plate of the capacitor?
Question 2.9 Explain what would happen if in the capacitor
given in Exercise2.8, a 3 mm thick mica sheet (of dielectric constant = 6) were
inserted between the plates,
(a) while the voltage supply remained connected.
(b) after the supply was disconnected.
Question 2.10 A 12pF capacitor is connected to a 50V battery.
How much electrostatic energy is stored in the capacitor?
Question 2.11 A 600pF capacitor is charged by a 200V supply.
It is then disconnected from the supply and is connected to another uncharged
600 pF capacitor. How much electrostatic energy is lost in the process?
ADDITIONAL EXERCISES QUESTIONS
Question 2.12 A charge of 8 mC is located at the origin.
Calculate the work done in taking a small charge of –2 × 10–9 C from a point P
(0, 0, 3 cm) to a point Q (0, 4 cm, 0), via a point R (0, 6 cm, 9 cm).
Question 2.13 A cube of side b has a charge q at each of its
vertices. Determine the potential and electric field due to this charge array at
the centre of the cube.
Question 2.14 Two tiny spheres carrying charges 1.5 μC and
2.5 μC are located 30 cm apart. Find the potential and electric field: (a) at
the mid-point of the line joining the two charges, and (b) at a point 10 cm from
this midpoint in a plane normal to the line and passing through the mid-point.
Question 2.15 A spherical conducting shell of inner radius
r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the centre of the shell. What is the surface
charge density on the inner and outer surfaces of the shell?
(b) Is the electric field inside a cavity (with no charge) zero, even if the
shell is not spherical, but has any irregular shape? Explain.
Question 2.16 (a) Show that the normal component of
electrostatic field has a discontinuity from one side of a charged surface to
another given by 2 1 0 ( ) ˆ σ ε E − E n = where ˆn is a unit vector normal to
the surface at a point and σ is the surface charge density at that point. (The
direction of ˆn is from side 1 to side 2.) Hence show that just outside a
conductor, the electric field is σ ˆn /ε0.
(b) Show that the tangential component of electrostatic field is continuous from
one side of a charged surface to another. [Hint: For (a), use Gauss’s law. For,
(b) use the fact that work done by electrostatic field on a closed loop is
zero.]
Question 2.17 A long charged cylinder of linear charged
density λ is surrounded by a hollow co-axial conducting cylinder. What is the
electric field in the space between the two cylinders?
Question 2.18 In a hydrogen atom, the electron and proton
are bound at a distance of about 0.53 Å:
(a) Estimate the potential energy of the system in eV, taking the zero of
the potential energy at infinite separation of the electron from proton.
(b) What is the minimum work required to free the electron, given that its
kinetic energy in the orbit is half the magnitude of potential energy obtained
in (a)?
(c) What are the answers to (a) and (b) above if the zero of potential energy is
taken at 1.06 Å separation?
Question 2.19 If one of the two electrons of a H2 molecule is
removed, we get a hydrogen molecular ion H+ 2.In the ground state of an H+ 2,
the two protons are separated by roughly 1.5 Å, and the electron is roughly 1 Å
from each proton. Determine the potential energy of the system. Specify your
choice of the zero of potential energy.
Question 2.20 Two charged conducting spheres of radii a and b
are connected to each other by a wire. What is the ratio of electric fields at
the surfaces of the two spheres? Use the result obtained to explain why charge
density on the sharp and pointed ends of a conductor is higher than on its
flatter portions.
Question 2.21 Two charges –q and +q are located at points
(0, 0, –a) and (0, 0, a), respectively.
(a) What is the electrostatic potential at the points (0, 0, z) and (x, y,
0) ?
(b) Obtain the dependence of potential on the distance r of a point from the
origin when r/a >> 1.
(c) How much work is done in moving a small test charge from the point (5,0,0)
to (–7,0,0) along the x-axis? Does the answer change if the path of the test
charge between the same points is not along the x-axis?
Question 2.22 Figure2.34 shows a charge array known as an
electric quadrupole. For a point on the axis of the quadrupole, obtain the
dependence of potential on r for r/a >> 1, and contrast your results with that
due to an electric dipole, and an electric monopole (i.e., a single charge).
Question 2.23 An electrical technician requires a capacitance
of 2 μF in a circuit across a potential difference of 1 kV. A large number of 1
μF capacitors are available to him each of which can withstand a potential
difference of not more than 400 V. Suggest a possible arrangement that requires
the minimum number of capacitors.
Question 2.24 What is the area of the plates of a 2 F
parallel plate capacitor, given that the separation between the plates is 0.5
cm? [You will realise from your answer why ordinary capacitors are in the range
of μF or less. However, electrolytic capacitors do have a much larger
capacitance (0.1 F) because of very minute separation between the conductors.]
Question 2.25 Obtain the equivalent capacitance of the
network in Fig. 2.35. For a 300 V supply, determine the charge and voltage
across each capacitor.
Question 2.26 The plates of a parallel plate capacitor have
an area of 90 cm2 each and are separated by 2.5 mm. The capacitor is charged by
connecting it to a 400 V supply.
(a) How much electrostatic energy is stored by the capacitor?
(b) View this energy as stored in the electrostatic field between the plates,
and obtain the energy per unit volume u. Hence arrive at a relation between u
and the magnitude of electric field E between the plates.
Question 2.27 A 4 μF capacitor is charged by a 200 V supply.
It is then disconnected from the supply, and is connected to another uncharged 2
μF capacitor. How much electrostatic energy of the first capacitor is lost in
the form of heat and electromagnetic radiation?
Question 2.28 Show that the force on each plate of a parallel
plate capacitor has a magnitude equal to (½) QE, where Q is the charge on the
capacitor, and E is the magnitude of electric field between the plates. Explain
the origin of the factor ½.
Question 2.29 A spherical capacitor consists of two
concentric spherical conductors, held in position by suitable insulating
supports (Fig2.36). Show that the capacitance of a spherical capacitor is given
by 0 1 2 1 2 4 – r r C r r πε = where r1 and r2 are the radii of outer and inner
spheres, respectively.
Question 2.30 A spherical capacitor has an inner sphere of
radius 12 cm and an outer sphere of radius 13 cm. The outer sphere is earthed
and the inner sphere is given a charge of 2.5 μC. The space between the
concentric spheres is filled with a liquid of dielectric constant 32.
(a) Determine the capacitance of the capacitor.
(b) What is the potential of the inner sphere?
(c) Compare the capacitance of this capacitor with that of an isolated sphere of
radius 12 cm. Explain why the latter is much smaller.s the magnitude of
electrostatic force between them exactly given by Q1 Q2/4πε0r 2, where r is the
distance between their centres?
(b) If Coulomb’s law involved 1/r3 dependence (instead of 1/r2), would Gauss’s
law be still true ?
(c) A small test charge is released at rest at a point in an electrostatic field
configuration. Will it travel along the field line passing through that point?
(d) What is the work done by the field of a nucleus in a complete circular orbit
of the electron? What if the orbit is elliptical?
(e) We know that electric field is discontinuous across the surface of a charged
conductor. Is electric potential also discontinuous there?
(f ) What meaning would you give to the capacitance of a single conductor?
(g) Guess a possible reason why water has a much greater dielectric constant (=
80) than say, mica (= 6).
Question 2.32 A cylindrical capacitor has two co-axial
cylinders of length 15 cm and radii 1.5 cm and 1.4 cm. The outer cylinder is
earthed and the inner cylinder is given a charge of 3.5 μC. Determine the
capacitance of the system and the potential of the inner cylinder. Neglect end
effects (i.e., bending of field lines at the ends).
Question 2.33 A parallel plate capacitor is to be designed
with a voltage rating 1 kV, using a material of dielectric constant 3 and
dielectric strength about 107 Vm–1. (Dielectric strength is the maximum electric
field a material can tolerate without breakdown, i.e., without starting to
conduct electricity through partial ionisation.) For safety, we should like the
field never to exceed, say 10% of the dielectric strength. What minimum area of
the plates is required to have a capacitance of 50 pF?
Question 2.34 Describe schematically the equipotential
surfaces corresponding to
(a) a constant electric field in the z-direction,
(b) a field that uniformly increases in magnitude but remains in a constant
(say, z) direction,
(c) a single positive charge at the origin, and
(d) a uniform grid consisting of long equally spaced parallel charged wires in a
plane .
Question 2.35 In a Van de Graaff type generator a spherical
metal shell is to be a 15 × 106 V electrode. The dielectric strength of the gas
surrounding the electrode is 5 × 107 Vm–1. What is the minimum radius of the
spherical shell required? (You will learn from this exercise why one cannot
build an electrostatic generator using a very small shell which requires a small
charge to acquire a high potential.)
Question 2.36 A small sphere of radius r1 and charge q1 is
enclosed by a spherical shell of radius r2 and charge q2. Show that if q1 is
positive, charge will necessarily flow from the sphere to the shell (when the
two are connected by a wire) no matter what the charge q2 on the shell is.
Question 2.37 Answer the following:
(a) The top of the atmosphere is at about 400 kV with respect to the surface
of the earth, corresponding to an electric field that decreases with altitude.
Near the surface of the earth, the field is about 100 Vm–1. Why then do we not
get an electric shock as we step out of our house into the open? (Assume the
house to be a steel cage so there is no field inside!)
(b) A man fixes outside his house one evening a two metre high insulating slab
carrying on its top a large aluminium sheet of area 1m 2.Will he get an electric
shock if he touches the metal sheet next morning?
(c) The discharging current in the atmosphere due to the small conductivity of
air is known to be 1800 A on an average over the globe. Why then does the
atmosphere not discharge itself completely in due course and become electrically
neutral? In other words, what keeps the atmosphere charged?
(d) What are the forms of energy into which the electrical energy of the
atmosphere is dissipated during a lightning? (Hint: The earth has an electric
field of about 100 Vm–1 at its surface in the downward direction, corresponding
to a surface charge density = –10–9 C m– 2. Due to the slight conductivity of
the atmosphere up to about 50 km (beyond which it is good conductor), about +
1800 C is pumped every second into the earth as a whole. The earth, however,
does not get discharged since thunderstorms and lightning occurring continually
all over the globe pump an equal amount of negative charge on the earth.)
:: Chapter 3 - Current Electricity ::
Question 3.1 The storage battery of a car has an emf of 12 V.
If the internal resistance of the battery is 0.4 Ω, what is the maximum current
that can be drawn from the battery?
Question 3.2 A battery of emf 10 V and internal resistance 3 Ω is connected to a
resistor. If the current in the circuit is 0.5 A, what is the resistance of the
resistor? What is the terminal voltage of the battery when the circuit is
closed?
Question 3.3 (a) Three resistors 1 Ω, 2 Ω, and 3 Ω are combined in series. What
is the total resistance of the combination? (b) If the combination is connected
to a battery of emf 12 V and negligible internal resistance, obtain the
potential drop across each resistor.
Question 3.4 (a) Three resistors 2 Ω, 4 Ω and 5 Ω are combined in parallel. What
is the total resistance of the combination?
(b) If the combination is connected to a battery of emf 20 V and negligible
internal resistance, determine the current through each resistor, and the total
current drawn from the battery.
Question 3.5 At room temperature (27.0 °C) the resistance of a heating element
is 100 Ω. What is the temperature of the element if the resistance is found to
be 117 Ω, given that the temperature coefficient of the material of the resistor
is 1.70 × 10–4 °C–1.
Question 3.6 A negligibly small current is passed through a wire of length 15 m
and uniform cross-section 6.0 × 10–7 m2, and its resistance is measured to be
5.0 Ω. What is the resistivity of the material at the temperature of the
experiment?
Question 3.7 A silver wire has a resistance of 2.1 Ω at 27.5 °C, and a
resistance of 2.7 Ω at 100 °C. Determine the temperature coefficient of
resistivity of silver.
Question 3.8 A heating element using nichrome connected to a 230 V supply draws
an initial current of 3.2 A which settles after a few seconds to a steady value
of 2.8 A. What is the steady temperature of the heating element if the room
temperature is 27.0 °C? Temperature coefficient of resistance of nichrome
averaged over the temperature range involved is 1.70 × 10–4 °C–1.
Question 3.9 Determine the current in each branch of the network shown in Fig.
3.30:
Question 3.10 (a) In a metre bridge [Fig. 3.7], the balance point is found to
be at 39.5 cm from the end A, when the resistor Y is of 12.5 Ω. Determine the
resistance of X. Why are the connections between resistors in a Wheatstone or
meter bridge made of thick copper strips?
(b) Determine the balance point of the bridge above if X and Y are
interchanged.
(c) What happens if the galvanometer and cell are interchanged at the balance
point of the bridge? Would the galvanometer show any current?
Question 3.11 A storage battery of emf 8.0 V and internal resistance 0.5 Ω is
being charged by a 120 V dc supply using a series resistor of 15.5 Ω. What is
the terminal voltage of the battery during charging? What is the purpose of
having a series resistor in the charging circuit?
Question 3.12 In a potentiometer arrangement, a cell of emf 1.25 V gives a
balance point at 35.0 cm length of the wire. If the cell is replaced by another
cell and the balance point shifts to 6 3.0 cm, what is the emf of the second
cell?
Question 3. 13 The number density of free electrons in a copper conductor
estimated in Example 3.1 is 8.5 × 1028 m–3. How long does an electron take to
drift from one end of a wire 3.0 m long to its other end? The area of
cross-section of the wire is 2.0 × 10–6 m2 and it is carrying a current of 3.0
A.
ADDITIONAL EXERCISES QUESTIONS
Question 3. 14 The earth’s surface has a negative surface
charge density of 10–9 C m–2. The potential difference of 400 kV between the top
of the atmosphere and the surface results (due to the low conductivity of the
lower atmosphere) in a current of only 1800 A over the entire globe. If there
were no mechanism of sustaining atmospheric electric field, how much time
(roughly) would be required to neutralise the earth’s surface? (This never
happens in practice because there is a mechanism to replenish electric charges,
namely the continual thunderstorms and lightning in different parts of the
globe). (Radius of earth = 6.37 × 106 m.)
Question 3.15 (a) Six lead-acid type of secondary cells each of emf 2.0 V and
internal resistance 0.015 Ω are joined in series to provide a supply to a
resistance of 8.5 Ω. What are the current drawn from the supply and its terminal
voltage?
(b) A secondary cell after long use has an emf of 1.9 V and a large internal
resistance of 380 Ω. What maximum current can be drawn from the cell? Could the
cell drive the starting motor of a car?
Question 3.16 Two wires of equal length, one of aluminium and the other of
copper have the same resistance. Which of the two wires is lighter? Hence
explain why aluminium wires are preferred for overhead power cables. (ρAl = 2.63
× 10–8 Ω m, ρCu = 1.72 × 10–8 Ω m, Relative density of Al = 2.7, of Cu = 8.9.)
Question 3.17 What conclusion can you draw from the following observations on a
resistor made of alloy manganin?
Question 3.18 Answer the following questions:
(a) A steady current flows in a metallic conductor of non-uniform
cross-section. Which of these quantities is constant along the conductor:
current, current density, electric field, drift speed?
(b) Is Ohm’s law universally applicable for all conducting elements? If not,
give examples of elements which do not obey Ohm’s law.
(c) A low voltage supply from which one needs high currents must have very low
internal resistance. Why?
(d) A high tension (HT) supply of, say, 6 kV must have a very large internal
resistance. Why?
Question 3.19 Choose the correct alternative:
(a) Alloys of metals usually have (greater/less) resistivity than that of
their constituent metals.
(b) Alloys usually have much (lower/higher) temperature coefficients of
resistance than pure metals.
(c) The resistivity of the alloy manganin is nearly independent of/ increases
rapidly with increase of temperature.
(d) The resistivity of a typical insulator (e.g., amber) is greater than that of
a metal by a factor of the order of (1022/103).
Question 3.20 (a) Given n resistors each of resistance R, how will you
combine them to get the
(i) maximum
(ii) minimum effective resistance? What is the ratio of the maximum to minimum
resistance? (b) Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them
to get an equivalent resistance of (i) (11/3) Ω (ii) (11/5) Ω,
(iii) 6 Ω, (iv) (6/11) Ω? (c) Determine the equivalent resistance of networks
shown in Fig. 3.31.
Question 3.22 Figure 3.33 shows a potentiometer with a cell of 2.0 V and
internal resistance 0.40 Ω maintaining a potential drop across the resistor wire
AB. A standard cell which maintains a constant emf of 1.02 V (for very moderate
currents upto a few mA) gives a balance point at 67.3 cm length of the wire. To
ensure very low currents drawn from the standard cell, a very high resistance of
600 kΩ is put in series with it, which is shorted close to the balance point.
The standard cell is then replaced by a cell of unknown emf ε and the balance
point found similarly, turns out to be at 82.3 cm length of the wire.
(c) Is the balance point affected by this high resistance?
(d) Is the balance point affected by the internal resistance of the driver cell?
(e) Would the method work in the above situation if the driver cell of the
potentiometer had an emf of 1.0V instead of 2.0V? (f ) Would the circuit work
well for determining an extremely small emf, say of the order of a few mV (such
as the typical emf of a thermo-couple)? If not, how will you modify the circuit?
Question 3.23 Figure 3.34 shows a potentiometer circuit for comparison of two
resistances. The balance point with a standard resistor R = 10.0 Ω is found to
be 58.3 cm, while that with the unknown resistance X is 68.5 cm. Determine the
value of X. What might you do if you failed to find a balance point with the
given cell of emf ε ?
Question 3.24 Figure 3.35 shows a 2.0 V potentiometer used for the determination
of internal resistance of a 1.5 V cell. The balance point of the cell in open
circuit is 76.3 cm. When a resistor of 9.5 Ω is used in the external circuit of
the cell, the balance point shifts to 64.8 cm length of the potentiometer wire.
Determine the internal resistance of the cell.
:: Chapter 4 - Moving Charges and Magnetism ::
Question 4.1 A circular coil of wire consisting of 100 turns,
each of radius 8.0 cm carries a current of 0.40 A. What is the magnitude of the
magnetic field B at the centre of the coil?
Question 4.2 A long straight wire carries a current of 35 A.
What is the magnitude of the field B at a point 20 cm from the wire?
Question 4.3 A long straight wire in the horizontal plane
carries a current of 50 A in north to south direction. Give the magnitude and
direction of B at a point 2.5 m east of the wire.
Question 4.4 A horizontal overhead power line carries a
current of 90 A in east to west direction. What is the magnitude and direction
of the magnetic field due to the current 1.5 m below the line?
Question 4.5 What is the magnitude of magnetic force per unit
length ?
Question 4.6 A 3.0 cm wire carrying a current of 10 A is
placed inside a solenoid perpendicular to its axis. The magnetic field inside
the solenoid is given to be 0.27 T. What is the magnetic force on the wire?
Question 4.7 Two long and parallel straight wires A and B
carrying currents of 8.0 A and 5.0 A in the same direction are separated by a
distance of 4.0 cm. Estimate the force on a 10 cm section of wire A.
Question 4.8 A closely wound solenoid 80 cm long has 5 layers
of windings of 400 turns each. The diameter of the solenoid is 1.8 cm. If the
current carried is 8.0 A, estimate the magnitude of B inside the solenoid near
its centre.
Question 4.9 A square coil of side 10 cm consists of 20 turns
and carries a current of 12 A. The coil is suspended vertically and the normal
to the plane of the coil makes an angle of 30º with the direction of a uniform
horizontal magnetic field of magnitude 0.80 T. What is the magnitude of torque
experienced by the coil?
Question 4.10 Two moving coil meters, M1 and M2 have the
following particulars: R1 = 10 Ω, N1 = 30, A1 = 3.6 × 10–3 m2, B1 = 0.25 T R2 =
14 Ω, N2 = 42, A2 = 1.8 × 10–3 m2, B2 = 0.50 T (The spring constants are
identical for the two meters). Determine the ratio of (a) current sensitivity
and (b) voltage sensitivity of M2 and M1.
Question 4.11 In a chamber, a uniform magnetic field of 6.5 G
(1 G = 10–4 T) is maintained. An electron is shot into the field
with a speed of 4.8 × 106 m s–1 normal to the field. Explain why the path of the
electron is a circle. Determine the radius of the circular orbit. (e = 1.6 ×
10–19 C, me = 9.1×10–31 kg)
Question 4.12 In Exercise 4.11 obtain the frequency of
revolution of the electron in its circular orbit. Does the answer depend on the
speed of the electron? Explain.
Question 4.13 (a) A circular coil of 30 turns and radius
8.0 cm carrying a current of 6.0 A is suspended vertically in a uniform
horizontal magnetic field of magnitude 1.0 T. The field lines make an angle of
60º with the normal of the coil. Calculate the magnitude of the counter torque
that must be applied to prevent the coil from turning.
(b) Would your answer change, if the circular coil in
(a) were replaced by a planar coil of some irregular shape that encloses the
same area? (All other particulars are also unaltered.)
ADDITIONAL EXERCISES QUESTION
Question 4.14 Two concentric circular coils X and Y of radii
16 cm and 10 cm, respectively, lie in the same vertical plane containing the
north to south direction. Coil X has 20 turns and carries a current of 16 A;
coil Y has 25 turns and carries a current of 18 A. The sense of the current in X
is anticlockwise, and clockwise in Y, for an observer looking at the coils
facing west. Give the magnitude and direction of the net magnetic field due to
the coils at their centre .
Question 4.15 A magnetic field of 100 G (1 G = 10–4 T) is
required which is uniform in a region of linear dimension about 10 cm and area
of cross-section about 10–3 m2. The maximum current-carrying capacity of a given
coil of wire is 15 A and the number of turns per unit length that can be wound
round a core is at most 1000 turns m–1. Suggest some appropriate design
particulars of a solenoid for the required purpose. Assume the core is not
ferromagnetic.
Question 4.16 For a circular coil of radius R and N turns
carrying current I, the magnitude of the magnetic field at a point on its axis
at a distance x from its centre is given by, ( ) 2 0 2 2 3/2 2 IR N B x R μ = +
(a) Show that this reduces to the familiar result for field at the centre of
the coil.
(b) Consider two parallel co-axial circular coils of equal radius R, and number
of turns N, carrying equal currents in the same direction, and separated by a
distance R. Show that the field on the axis around the mid-point between the
coils is uniform over a distance that is small as compared to R, and is given
by, 0.72 0 NI B R μ = , approximately. [Such an arrangement to produce a nearly
uniform magnetic field over a small region is known as Helmholtz coils.]
Question 4.17 A toroid has a core (non-ferromagnetic) of
inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are
wound. If the current in the wire is 11 A, what is the magnetic field (a)
outside the toroid, (b) inside the core of the toroid, and (c) in the empty
space surrounded by the toroid.
Question 4.18 Answer the following questions:
(a) A magnetic field that varies in magnitude from point to point but has a
constant direction (east to west) is set up in a chamber. A charged particle
enters the chamber and travels undeflectedalong a straight path with constant
speed. What can you say about the initial velocity of the particle?
(b) A charged particle enters an environment of a strong and non-uniform
magnetic field varying from point to point both in magnitude and direction, and
comes out of it following a complicated trajectory. Would its final speed equal
the initial speed if it suffered no collisions with the environment?
(c) An electron travelling west to east enters a chamber having a uniform
electrostatic field in north to south direction. Specify the direction in which
a uniform magnetic field should be set up to prevent the electron from
deflecting from its straight line path.
Question 4.19 An electron emitted by a heated cathode and accelerated through
a potential difference of 2.0 kV, enters a region with uniform magnetic field of
0.15 T. Determine the trajectory of the electron if the field
(a) is transverse to its initial velocity,
(b) makes an angle of 30º with the initial velocity.
Question 4.20 A magnetic field set up using Helmholtz coils
(described in Exercise 4.16) is uniform in a small region and has a magnitude of
0.75 T. In the same region, a uniform electrostatic field is maintained in a
direction normal to the common axis of the coils. A narrow beam of (single
species) charged particles all accelerated through 15 kV enters this region in a
direction perpendicular to both the axis of the coils and the electrostatic
field. If the beam remains undeflected when the electrostatic field is 9.0 ×
10–5 V m–1, make a simple guess as to what the beam contains. Why is the answer
not unique?
Question 4.21 A straight horizontal conducting rod of length 0.45 m and mass
60 g is suspended by two vertical wires at its ends. A current of 5.0 A is set
up in the rod through the wires.
(a) What magnetic field should be set up normal to the conductor in order
that the tension in the wires is zero?
(b) What will be the total tension in the wires if the direction of current is
reversed keeping the magnetic field same as before? (Ignore the mass of the
wires.) g = 9.8 m s–2.
Question 4.22 The wires which connect the battery of an
automobile to its starting motor carry a current of 300 A (for a short time).
What is the force per unit length between the wires if they are 70 cm long and
1.5 cm apart? Is the force attractive or repulsive?
Question 4.23 A uniform magnetic field of 1.5 T exists in
a cylindrical region of radius10.0 cm, its direction parallel to the axis along
east to west. A wire carrying current of 7.0 A in the north to south direction
passes through this region. What is the magnitude and direction of the force on
the wire if,
(a) the wire intersects the axis,
(b) the wire is turned from N-S to northeast-northwest direction,
(c) the wire in the N-S direction is lowered from the axis by a distance of 6.0
cm?
Question 4.24 A uniform magnetic field of 3000 G is
established along the positive z-direction. A rectangular loop of sides 10 cm
and 5 cm carries a current of 12 A. What is the torque on the loop in the
different cases shown in Fig. 4.28? What is the force on each case? Which case
corresponds to stable equilibrium?
Question 4.25 A circular coil of 20 turns and radius 10 cm
is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil.
If the current in the coil is 5.0 A, what is the
(a) total torque on the coil,
(b) total force on the coil,
(c) average force on each electron in the coil due to the magnetic field? (The
coil is made of copper wire of cross-sectional area 10–5 m2, and the free
electron density in copper is given to be about 1029 m–3.)
Question 4.26 A solenoid 60 cm long and of radius 4.0 cm has
3 layers of windings of 300 turns each. A 2.0 cm long wire of mass 2.5 g lies
inside the solenoid (near its centre) normal to its axis; both the wire and the
axis of the solenoid are in the horizontal plane. The wire is connected through
two leads parallel to the axis of the solenoid to an external battery which
supplies a current of 6.0 A in the wire. What value of current (with appropriate
sense of circulation) in the windings of the solenoid can support the weight of
the wire? g = 9.8 m s–2.
Question 4.27 A galvanometer coil has a resistance of 12 Ω
and the metre shows full scale deflection for a current of 3 mA. How will you
convert the metre into a voltmeter of range 0 to 18 V?
Question 4.28 A galvanometer coil has a resistance of 15 Ω
and the metre shows full scale deflection for a current of 4 mA. How will you
convert the metre into an ammeter of range 0 to 6 A?
:: Chapter 5 - Magnetism and Matter ::
Question 5.1 Answer the following questions regarding
earth’s magnetism:
(a) A vector needs three quantities for its specification. Name the three
independent quantities conventionally used to specify the earth’s magnetic
field.
(b) The angle of dip at a location in southern India is about 18º. Would you
expect a greater or smaller dip angle in Britain?
(c) If you made a map of magnetic field lines at Melbourne in Australia, would
the lines seem to go into the ground or come out of the ground?
(d) In which direction would a compass free to move in the vertical plane point
to, if located right on the geomagnetic north or south pole?
(e) The earth’s field, it is claimed, roughly approximates the field due to a
dipole of magnetic moment 8 × 1022 J T–1 located at its centre. Check the order
of magnitude of this number in some way.
(f ) Geologists claim that besides the main magnetic N-S poles, there are
several local poles on the earth’s surface oriented in different directions. How
is such a thing possible at all?
Question 5.2 Answer the following questions:
(a) The earth’s magnetic field varies from point to point in space. Does it
also change with time? If so, on what time scale does it change appreciably?
(b) The earth’s core is known to contain iron. Yet geologists do not regard this
as a source of the earth’s magnetism. Why?
(c) The charged currents in the outer conducting regions of the earth’s core are
thought to be responsible for earth’s magnetism. What might be the ‘battery’
(i.e., the source of energy) to sustain these currents?
(d) The earth may have even reversed the direction of its field several times
during its history of 4 to 5 billion years. How can geologists know about the
earth’s field in such distant past?
(e) The earth’s field departs from its dipole shape substantially at large
distances (greater than about 30,000 km). What agencies may be responsible for
this distortion?
(f ) Interstellar space has an extremely weak magnetic field of the order of
10–12 T. Can such a weak field be of any significant consequence?
Question 5.2 is meant mainly to arouse your curiosity.
Answers to some questions above are tentative or unknown. Brief answers wherever
possible are given at the end. For details, you should consult a good text on
geomagnetism.]
Question 5.3 A short bar magnet placed with its axis at 30º
with a uniform external magnetic field of 0.25 T experiences a torque of
magnitude equal to 4.5 × 10–2 J. What is the magnitude of magnetic moment of the
magnet?
Question 5.4 A short bar magnet of magnetic moment m = 0.32
JT–1 is placed in a uniform magnetic field of 0.15 T. If the bar is free to
rotate in the plane of the field, which orientation wou
Question 5.5 A closely wound solenoid of 800 turns and area
of cross section 2.5 × 10–4 m2 carries a current of 3.0 A. Explain the sense in
which the solenoid acts like a bar magnet. What is its associated magnetic
moment?
Question 5.6 If the solenoid in xercise 5.5 is free to turn
about the vertical direction and a uniform horizontal magnetic field of 0.215 T
is applied, what is the magnitude of torque on the solenoid when its axis makes
an angle of 30° with the direction of applied field?
Question 5.7 A bar magnet of magnetic moment 1.5 J T–1
lies aligned with the direction of a uniform magnetic field of 0.22 T. (a) What
is the amount of work required by an external torque to turn the magnet so as to
align its magnetic moment:
(i) normal to the field direction , (ii) opposite to the field direction?
(b) What is the torque on the magnet in cases (i) and (ii)?
Question 5.8 A closely wound solenoid of 2000 turns and
area of cross-section 1.6 × 10–4 m2, carrying a current of 4.0 A, is suspended
through its centre allowing it to turn in a horizontal plane.
(a) What is the magnetic moment associated with the solenoid?
(b) What is the force and torque on the solenoid if a uniform horizontal
magnetic field of 7.5 × 10–2 T is set up at an angle of 30º with the axis of the
solenoid?
Question 5.9 A circular coil of 16 turns and radius 10 cm
carrying a current of 0.75 A rests with its plane normal to an external field of
magnitude 5.0 × 10–2 T. The coil is free to turn about an axis in its plane
perpendicular to the field direction. When the coil is turned slightly and
released, it oscillates about its stable equilibrium with a frequency of 2.0
s–1. What is the moment of inertia of the coil about its axis of rotation?
Question 5.10 A magnetic needle free to rotate in a vertical
plane parallel to the magnetic meridian has its north tip pointing down at 22º
with the horizontal. The horizontal component of the earth’s magnetic field at
the place is known to be 0.35 G. Determine the magnitude of the earth’s magnetic
field at the place.
Question 5.11 At a certain location in Africa, a compass
points 12º west of the geographic north. The north tip of the magnetic needle of
a dip circle placed in the plane of magnetic meridian points 60º above the
horizontal. The horizontal component of the earth’s field is measured to be 0.16
G. Specify the direction and magnitude of the earth’s field at the location.
Question 5.12 A short bar magnet has a magnetic moment of
0.48 J T–1. Give the direction and magnitude of the magnetic field produced by
the magnet at a distance of 10 cm from the centre of the magnet on (a) the
axis,(b) the equatorial lines (normal bisector) of the magnet.
Question 5.13 A short bar magnet placed in a horizontal plane
has its axis aligned along the magnetic north-south direction. Null points are
found on the axis of the magnet at 14 cm from the centre of the magnet. The
earth’s magnetic field at the place is 0.36 G and the angle of dip is zero. What
is the total magnetic field on the normal bisector of the magnet at the same
distance as the null–point (i.e., 14 cm) from the centre of the magnet? (At null
points, field due to a magnet is equal and opposite to the horizontal component
of earth’s magnetic field.)
Question 5.14 If the bar magnet in exercise 5.13 is turned
around by 180º, where will the new null points be located?
Question 5.15 A short bar magnet of magnetic moment 5.25 ×
10–2 J T–1 is placed with its axis perpendicular to the earth’s field direction.
At what distance from the centre of the magnet, the resultant field is inclined
at 45º with earth’s field on (a) its normal bisector and (b) its axis. Magnitude
of the earth’s field at the place is given to be 0.42 G. Ignore the length of
the magnet in comparison to the distances involved.
ADDITIONAL EXERCISES QUESTIONS
Question 5.16 Answer the following questions:
(a) Why does a paramagnetic sample display greater magnetisation (for the
(c) If a toroid uses bismuth for its core, will the field in the core be
(slightly) greater or (slightly) less than when the core is empty?
(d) Is the permeability of a ferromagnetic material independent of the magnetic
field? If not, is it more for lower or higher fields?
(e) Magnetic field lines are always nearly normal to the surface of a
ferromagnet at every point. (This fact is analogous to the static electric field
lines being normal to the surface of a conductor at every point.) Why?
(f ) Would the maximum possible magnetisation of a paramagnetic sample be of the
same order of magnitude as the magnetisation of a ferromagnet?
Question 5.17 Answer the following questions:
(a) Explain qualitatively on the basis of domain picture the irreversibility
in the magnetisation curve of a ferromagnet.
(b) The hysteresis loop of a soft iron piece has a much smaller area than that
of a carbon steel piece. If the material is to go through repeated cycles of
magnetisation, which piece will dissipate greater heat energy?
(c) ‘A system displaying a hysteresis loop such as a ferromagnet, is a device
for storing memory?’ Explain the meaning of this statement.
(d) What kind of ferromagnetic material is used for coating magnetic tapes in a
cassette player, or for building ‘memory stores’ in a modern computer?
(e) A certain region of space is to be shielded from magnetic fields. Suggest a
method .
Question 5.18 A long straight horizontal cable carries a
current of 2.5 A in the direction 10º south of west to 10º north of east. The
magnetic meridian of the place happens to be 10º west of the geographic
meridian. The earth’s magnetic field at the location is 0.33 G, and the angle of
dip is zero. Locate the line of neutral points (ignore the thickness of the
cable). (At neutral points, magnetic field due to a current-carrying cable is
equal and opposite to the horizontal component of earth’s magnetic field.)
Question 5.19 A telephone cable at a place has four long
straight horizontal wires carrying a current of 1.0 A in the same direction east
to west. The earth’s magnetic field at the place is 0.39 G, and the angle of dip
is 35º. The magnetic declination is nearly zero. What are the resultant magnetic
fields at points 4.0 cm below the cable?
Question 5.20 A compass needle free to turn in a
horizontal plane is placed at the centre of circular coil of 30 turns and radius
12 cm. The coil is in a vertical plane making an angle of 45º with the magnetic
meridian. When the current in the coil is 0.35 A, the needle points west to
east.
(a) Determine the horizontal component of the earth’s magnetic field at the
location.
(b) The current in the coil is reversed, and the coil is rotated about its
vertical axis by an angle of 90º in the anticlockwise sense looking from above.
Predict the direction of the needle. Take the magnetic declination at the places
to be zero.
Question 5.21 A magnetic dipole is under the influence of two
magnetic fields. The angle between the field directions is 60º, and one of the
fields has a magnitude of 1.2 × 10–2 T. If the dipole comes to stable
equilibrium at an angle of 15º with this field, what is the magnitude of the
other field?
Question 5.22 A monoenergetic (18 keV) electron beam
initially in the horizontal direction is subjected to a horizontal magnetic
field of 0.04 G normal to the initial direction. Estimate the up or down
deflection of the beam over a distance of 30 cm (me = 9.11 × 10–19 C). [Note:
Data in this exercise are so chosen that the answer will give you an idea of the
effect of earth’s magnetic field on the motion of the electron beam from the
electron gun to the screen in a TV set.]
Question 5.23 A sample of paramagnetic salt contains 2.0 ×
1024 atomic dipoles each of dipole moment 1.5 × 10–23 J T–1. The sample is
placed under a homogeneous magnetic field of 0.64 T, and cooled to a temperature
of 4.2 K. The degree of magnetic saturation achieved is equal to 15%. What is
the total dipole moment of the sample for a magnetic field of 0.98 T and a
temperature of 2.8 K? (Assume Curie’s law
Question 5.24 A Rowland ring of mean radius 15 cm has 3500
turns of wire wound on a ferromagnetic core of relative permeability 800. What
is the magnetic field B in the core for a magnetising current of 1.2 A?
Question 5.25 The magnetic moment vectors μs and μl
associated with the intrinsic spin angular momentum S and orbital angular
momentum l, respectively, of an electron are predicted by quantum theory (and
verified experimentally to a high accuracy) to be given by: μs = –(e/m) S, μl =
–(e/2m)l Which of these relations is in accordance with the result expected
classically? Outline the derivation of the classical result
:: Chapter 6 - Electromagnetic Induction ::
Question 6.1 Predict the direction of induced current in
the situations described by the following Figs. 6.18(a) to (f ).
Question 6.2 Use Lenz’s law to determine the direction of
induced current in the situations described by Fig. 6.19:
(a) A wire of irregular shape turning into a circular shape;
(b) A circular loop being deformed into a narrow straight wire.
Question 6.3 A long solenoid with 15 turns per cm has a small
loop of area 2.0 cm2 placed inside the solenoid normal to its axis. If the
current carried by the solenoid changes steadily from 2.0 A to 4.0 A in 0.1 s,
what is the induced emf in the loop while the current is changing?
Question 6.4 A rectangular wire loop of sides 8 cm and 2 cm
with a small cut is moving out of a region of uniform magnetic field of
magnitude 0.3 T directed normal to the loop. What is the emf developed across
the cut if the velocity of the loop is 1 cm s–1 in a direction normal to the (a)
longer side, (b) shorter side of the loop? For how long does the induced voltage
last in each case?
Question 6.5 A 1.0 m long metallic rod is rotated with an
angular frequency of 400 rad s–1 about an axis normal to the rod passing through
its one end. The other end of the rod is in contact with a circular metallic
ring. A constant and uniform magnetic field of 0.5 T parallel to the axis exists
everywhere. Calculate the emf developed between the centre and the ring.
Question 6.6 A circular coil of radius 8.0 cm and 20 turns is
rotated about its vertical diameter with an angular speed of 50 rad s–1 in a
uniform horizontal magnetic field of magnitude 3.0 × 10–2 T. Obtain the maximum
and average emf induced in the coil. If the coil forms a closed loop of
resistance 10 Ω, calculate the maximum value of current in the coil. Calculate
the average power loss due to Joule heating. Where does this power come from?
Question 6.7 A horizontal straight wire 10 m long
extending from east to west is falling with a speed of 5.0 m s–1, at right
angles to the horizontal component of the earth’s magnetic field, 0.30 × 10–4 Wb
m–2.
(a) What is the instantaneous value of the emf induced in the wire?
(b) What is the direction of the emf?
(c) Which end of the wire is at the higher electrical potential?
Question 6.8 Current in a circuit falls from 5.0 A to 0.0 A
in 0.1 s. If an average emf of 200 V induced, give an estimate of the
self-inductance of the circuit.
Question 6.9 A pair of adjacent coils has a mutual inductance
of 1.5 H. If the current in one coil changes from 0 to 20 A in 0.5 s, what is
the change of flux linkage with the other coil?
Question 6.10 A jet plane is travelling towards west at a
speed of 1800 km/h. What is the voltage difference developed between the ends of
the wing
ADDITIONAL EXERCISES QUESTIONS
Question 6.11 Suppose the loop in Exercise Question 6.4 is
stationary but the current feeding the electromagnet that produces the magnetic
field is gradually reduced so that the field decreases from its initial value of
0.3 T at the rate of 0.02 T s–1. If the cut is joined and the loop has a
resistance of 1.6 Ω, how much power is dissipated by the loop as heat? What is
the source of this power?
Question 6.12 A square loop of side 12 cm with its sides
parallel to X and Y axes is moved with a velocity of 8 cm s–1 in the positive
x-direction in an environment containing a magnetic field in the positive
z-direction. The field is neither uniform in space nor constant in time. It has
a gradient of 10 –3 T cm–1 along the negative x-direction (that is it increases
by 10 – 3 T cm–1 as one moves in the negative x-direction), and it is decreasing
in time at the rate of 10 –3 T s–1. Determine the direction and magnitude of the
induced current in the loop if its resistance is 4.50 mΩ.
Question 6.13 It is desired to measure the magnitude of field
between the poles of a powerful loud speaker magnet. A small flat search coil of
area 2 cm2 with 25 closely wound turns, is positioned normal to the field
direction, and then quickly snatched out of the field region. Equivalently, one
can give it a quick 90° turn to bring its plane parallel to the field
direction). The total charge flown in the coil (measured by a ballistic
galvanometer connected to coil) is 7.5 mC. The combined resistance of the coil
and the galvanometer is 0.50 Ω. Estimate the field strength of magnet.
Question 6.14 Figure 6.20 shows a metal rod PQ resting on
the smooth rails AB and positioned between the poles of a permanent magnet. The
rails, the rod, and the magnetic field are in three mutual perpendicular
directions. A galvanometer G connects the rails through a switch K. Length of
the rod = 15 cm, B = 0.50 T, resistance of the closed loop containing the rod =
9.0 mΩ. Assume the field to be uniform.
(a) Suppose K is open and the rod is moved with a speed of 12 cm s–1 in the
direction shown. Give the polarity and magnitude of the induced emf. experience
magnetic force due to the motion of the rod. Explain.
(d) What is the retarding force on the rod when K is closed?
(e) How much power is required (by an external agent) to keep the rod moving at
the same speed (=12 cm s–1) when K is closed? How much power is required when K
is open?
(f ) How much power is dissipated as heat in the closed circuit? What is the
source of this power?
(g) What is the induced emf in the moving rod if the magnetic field is parallel
to the rails instead of being perpendicular?
Question 6.15 An air-cored solenoid with length 30 cm, area
of cross-section 25 cm2 and number of turns 500, carries a current of 2.5 A. The
current is suddenly switched off in a brief time of 10–3 s. How much is the
average back emf induced across the ends of the open switch in the circuit?
Ignore the variation in magnetic field near the ends of the solenoid.
Question 6.16 (a) Obtain an expression for the mutual
inductance between a long straight wire and a square loop of side a as shown in
Fig. 6.21.
(b) Now assume that the straight wire carries a current of 50 A and the loop is
moved to the right with a constant velocity, v = 10 m/s. Calculate the induced
emf in the loop at the instant when x = 0.2 m. Take a = 0.1 m and assume that
the loop has a large resistance.
Question 6.17 A line charge λ per unit length is lodged
uniformly onto the rim of a wheel of mass M and radius R. The wheel has light
non-conducting spokes and is free to rotate without friction about its axis
(Fig. 6.22). A uniform magnetic field extends over a circular region within the
rim. It is given by, B = – B0 k (r ≤ a; a < R) = 0 (otherwise) What is the
angular velocity of the wheel after the field is suddenly switched off?
:: Chapter 7 - Alternating Current ::
Question 7.1 A 100 Ω resistor is connected to a 220 V, 50
Hz ac supply.
(a) What is the rms value of current in the circuit?
(b) What is the net power consumed over a full cycle?
Question 7.2(a) The peak voltage of an ac supply is 300 V.
What is the rms voltage?
(b) The rms value of current in an ac circuit is 10 A. What is the peak current?
Question 7.3 A 44 mH inductor is connected to 220 V, 50 Hz ac
supply. Determine the rms value of the current in the circuit.
Question 7.4 A 60 μF capacitor is connected to a 110 V, 60 Hz
ac supply. Determine the rms value of the current in the circuit.
Question 7.5 In Exercises 7.3 and 7.4, what is the net power
absorbed by each circuit over a complete cycle. Explain your answer.
Question 7.6 Obtain the resonant frequency ωr of a series LCR
circuit with L = 2.0H, C = 32 μF and R = 10 Ω. What is the Q-value of this
circuit?
Question 7.7 A charged 30 μF capacitor is connected to a 27
mH inductor. What is the angular frequency of free oscillations of the circuit?
Question 7.8 Suppose the initial charge on the capacitor in
Exercise
Question 7.7 is 6 mC. What is the total energy stored in the
circuit initially? What is the total energy at later time?
Question 7.9 A series LCR circuit with R = 20 Ω, L = 1.5 H
and C = 35 μF is connected to a variable-frequency 200 V ac supply. When the
frequency of the supply equals the natural frequency of the circuit, what is the
average power transferred to the circuit in one complete cycle?
Question 7.10 A radio can tune over the frequency range of a
portion of MW broadcast band: (800 kHz to 1200 kHz). If its LC circuit has an
effective inductance of 200 μH, what must be the range of its variable
capacitor? [Hint: For tuning, the natural frequency i.e., the frequency of free
oscillations of the LC circuit should be equal to the frequency of the radiowave.]
Question 7.11 Figure 7.21 shows a series LCR circuit
connected to a variable frequency 230 V source. L = 5.0 H, C = 80μF, R = 40 Ω.
(a) Determine the source frequency which drives the circuit in resonance.
(b) Obtain the impedance of the circuit and the amplitude of current at the
resonating frequency.
(c) Determine the rms potential drops across the three elements of the circuit.
Show that the potential drop across the LC combination is zero at the resonating
frequency.
ADDITIONAL EXERCISES QUESTIONS
Question 7.12 An LC circuit contains a 20 mH inductor and
a 50 μF capacitor with an initial charge of 10 mC. The resistance of the circuit
is negligible. Let the instant the circuit is closed be t = 0 .
(a) What is the total energy stored initially? Is it conserved during LC
oscillations?
(b) What is the natural frequency of the circuit?
(c) At what time is the energy stored
(i) completely electrical (i.e., stored in the capacitor)?
(ii) completely magnetic (i.e., stored in the inductor)?
(d) At what times is the total energy shared equally between the inductor and
the capacitor?
(e) If a resistor is inserted in the circuit, how much energy is eventually
dissipated as heat?
Question 7.13 A coil of inductance 0.50 H and resistance
100 Ω is connected to a 240 V, 50 Hz ac supply.
(a) What is the maximum current in the coil?
(b) What is the time lag between the voltage maximum and the current maximum?
Question 7.14 Obtain the answers (a) to (b) in Exercise 7.13
if the circuit is connected to a high frequency supply (240 V, 10 kHz). Hence,
explain the statement that at very high frequency, an inductor in a circuit
nearly amounts to an open circuit. How does an inductor behave in a dc circuit
after the steady state?
Question 7.15 A 100 μF capacitor in series with a 40 Ω
resistance is connected to a 110 V, 60 Hz supply.
(a) What is the maximum current in the circuit?
(b) What is the time lag between the current maximum and the voltage maximum?
Question 7.16 Obtain the answers to (a) and (b) in Exercise
7.15 if the circuit is connected to a 110 V, 12 kHz supply? Hence, explain the
statement that a capacitor is a conductor at very high frequencies. Compare this
behaviour with that of a capacitor in a dc circuit after the steady state.
Question 7.17 Keeping the source frequency equal to the
resonating frequency of the series LCR circuit, if the three elements, L, C and
R are arranged in parallel, show that the total current in the parallel LCR
circuit is minimum at this frequency. Obtain the current rms value in each
branch of the circuit for the elements and source specified in Exercise 7.11 for
this frequency.
Question 7.18 A circuit containing a 80 mH inductor and a
60 μF capacitor in series is connected to a 230 V, 50 Hz supply. The resistance
of the circuit is negligible.
(a) Obtain the current amplitude and rms values
(b) Obtain the rms values of potential drops across each element.
(c) What is the average power transferred to the inductor?
(d) What is the average power transferred to the capacitor?
(e) What is the total average power absorbed by the circuit? [‘Average’ implies
‘averaged over one cycle’.]
Question 7.19 Suppose the circuit in Exercise 7.18 has a
resistance of 15 Ω. Obtain the average power transferred to each element of the
circuit, and the total power absorbed. Physics 268
Question 7.20 A series LCR circuit with L = 0.12 H, C =
480 nF, R = 23 Ω is connected to a 230 V variable frequency supply.
(a) What is the source frequency for which current amplitude is maximum.
Obtain this maximum value.
(b) What is the source frequency for which average power absorbed by the circuit
is maximum. Obtain the value of this maximum power.
(c) For which frequencies of the source is the power transferred to the circuit
half the power at resonant frequency? What is the current amplitude at these
frequencies?
(d) What is the Q-factor of the given circuit?
Question 7.21 Obtain the resonant frequency and Q-factor of a
series LCR circuit with L = 3.0 H, C = 27 μF, and R = 7.4 Ω. It is desired to
improve the sharpness of the resonance of the circuit by reducing its ‘full
width at half maximum’ by a factor of 2. Suggest a suitable way.
Question 7.22 Answer the following questions:
(a) In any ac circuit, is the applied instantaneous voltage equal to the
algebraic sum of the instantaneous voltages across the series elements of the
circuit? Is the same true for rms voltage?
(b) A capacitor is used in the primary circuit of an induction coil.
(c) An applied voltage signal consists of a superposition of a dc voltage and an
ac voltage of high frequency. The circuit consists of an inductor and a
capacitor in series. Show that the dc signal will appear across C and the
ac signal across L.
(d) A choke coil in series with a lamp is connected to a dc line. The lamp is
seen to shine brightly. Insertion of an iron core in the choke causes no change
in the lamp’s brightness. Predict the corresponding observations if the
connection is to an ac line.
(e) Why is choke coil needed in the use of fluorescent tubes with ac mains? Why
can we not use an ordinary resistor instead of the choke coil?
Question 7.23 A power transmission line feeds input power at
2300 V to a stepdown transformer with its primary windings having 4000 turns.
What should be the number of turns in the secondary in order to get output power
at 230 V?
Question 7.24 At a hydroelectric power plant, the water
pressure head is at a height of 300 m and the water flow available is 100 m3s–1.
If the turbine generator efficiency is 60%, estimate the electric power
available from the plant (g = 9.8 ms–2 ).
Question 7.25 A small town with a demand of 800 kW of
electric power at 220 V is situated 15 km away from an electric plant generating
power at 440 V. The resistance of the two wire line carrying power is 0.5 Ω per
km. The town gets power from the line through a 4000-220 V step-down transformer
at a sub-station in the town.
(a) Estimate the line power loss in the form of heat.
(b) How much power must the plant supply, assuming there is negligible power
loss due to leakage?
(c) Characterise the step up transformer at the plant.
Question 7.26 Do the same exercise as above with the
replacement of the earlier transformer by a 40,000-220 V step-down transformer
(Neglect, as before, leakage losses though this may not be a good assumption any
longer because of the very high voltage transmission involved). Hence, explain
why high voltage transmission is preferred?
:: Chapter 8 - Electromagnetic Waves ::
Question 8.1 Figure 8.6 shows a capacitor made of
two circular plates each of radius 12 cm, and separated by 5.0 cm. The capacitor
is being charged by an external source (not shown in the figure). The charging
current is constant and equal to 0.15A.
(a) Calculate the capacitance and the rate of charge of
potential difference between the plates.
(b) Obtain the displacement current across the plates.
(c) Is Kirchhoff’s first rule (junction rule) valid at each plate of the
capacitor? Explain
Question 8.2 A parallel plate capacitor (Fig. 8.7) made of circular plates
each of radius R = 6.0 cm has a capacitance C = 100 pF. The capacitor is
connected to a 230 V ac supply with a (angular) frequency of 300 rad s–1.
(a) What is the rms value of the conduction current?
(b) Is the conduction current equal to the displacement current?
(c) Determine the amplitude of B at a point 3.0 cm from the axis between the
plates.
Question 8.3 What physical quantity is the same for X-rays of
wavelength 10–10 m, red light of wavelength 6800 Å and radiowaves of wavelength
500m?
Question 8.4 A plane electromagnetic wave travels in vacuum
along z-direction. What can you say about the directions of its electric and
magnetic field vectors? If the frequency of the wave is 30 MHz, what is its
wavelength?
Question 8.5 A radio can tune in to any station in the 7.5
MHz to 12 MHz band. What is the corresponding wavelength band?
Question 8.6 A charged particle oscillates about its mean
equilibrium position with a frequency of 109 Hz. What is the frequency of the
electromagnetic waves produced by the oscillator?
Question 8.7 The amplitude of the magnetic field part of a
harmonic electromagnetic wave in vacuum is B0 = 510 nT. What is the amplitude of
the electric field part of the wave?
Question 8.8 Suppose that the electric field amplitude of
an electromagnetic wave is E0 = 120 N/C and that its frequency is ν = 50.0 MHz.
(a) Determine, B0,ω, k, and λ
(b) Find expressions for E and B.
Question 8.9 The terminology of different parts of the
electromagnetic spectrum is given in the text. Use the formula E = hν (for
energy of a quantum of radiation: photon) and obtain the photon energy in units
of eV for different parts of the electromagnetic spectrum. In what way are the
different scales of photon energies that you obtain related to the sources of
electromagnetic radiation?
Question 8.10 In a plane electromagnetic wave, the
electric field oscillates sinusoidally at a frequency of 2.0 × 1010 Hz and
amplitude 48 V m–1.
(a) What is the wavelength of the wave?
(b) What is the amplitude of the oscillating magnetic field? (c) Show that the
average energy density of the E field equals the average energy density of the B
field. [c = 3 × 108 m s–1.]
ADDITIONAL EXERCISES
Question 8.11 Suppose that the electric field part of an
electromagnetic wave in vacuum is E = {(3.1 N/C) cos [(1.8 rad/m) y + (5.4 × 106
rad/s)t]}ˆi .
(a) What is the direction of propagation?
(b) What is the wavelength λ ?
(c) What is the frequency ν ?
(d) What is the amplitude of the magnetic field part of the wave?
(e) Write an expression for the magnetic field part of the wave.
Question 8.12 About 5% of the power of a 100 W light bulb
is converted to visible radiation. What is the average intensity of visible
radiation
(a) at a distance of 1m from the bulb?
(b) at a distance of 10 m? Assume that the radiation is emitted isotropically
and neglect reflection.
Question 8.13 Use the formula λm T = 0.29 cmK to obtain the
characteristic temperature ranges for different parts of the electromagnetic
spectrum. What do the numbers that you obtain tell you?
Question 8.14 Given below are some famous numbers
associated with electromagnetic radiations in different contexts in physics.
State the part of the electromagnetic spectrum to which each belongs.
(a) 21 cm (wavelength emitted by atomic hydrogen in interstellar space).
(b) 1057 MHz (frequency of radiation arising from two close energy levels in
hydrogen; known as Lamb shift).
(c) 2.7 K [temperature associated with the isotropic radiation filling all
space-thought to be a relic of the ‘big-bang’ origin of the universe].
(d) 5890 Å - 5896 Å [double lines of sodium]
(e) 14.4 keV [energy of a particular transition in 57Fe nucleus associated with
a famous high resolution spectroscopic method (Mössbauer spectroscopy)].
Question 8.15 Answer the following questions:
(a) Long distance radio broadcasts use short-wave bands. Why?
(b) It is necessary to use satellites for long distance TV transmission. Why?
(c) Optical and radiotelescopes are built on the ground but X-ray astronomy is
possible only from satellites orbiting the earth. Why?
(d) The small ozone layer on top of the stratosphere is crucial for human
survival. Why?
(e) If the earth did not have an atmosphere, would its average surface
temperature be higher or lower than what it is now?
(f ) Some scientists have predicted that a global nuclear war on the earth would
be followed by a severe ‘nuclear winter’ with a devastating effect on life on
earth. What might be the basis of this prediction?
:: Chapter 9 - Ray Optics and Optical Instruments ::
Question 9.1 A small candle, 2.5 cm in size is placed at 27
cm in front of a concave mirror of radius of curvature 36 cm. At what distance
from the mirror should a screen be placed in order to obtain a sharp image?
Describe the nature and size of the image. If the candle is moved closer to the
mirror, how would the screen have to be moved?
Question 9.2 A 4.5 cm needle is placed 12 cm away from a
convex mirror of focal length 15 cm. Give the location of the image and the
magnification. Describe what happens as the needle is moved farther from the
mirror.
Question 9.3 A tank is filled with water to a height of 12.5
cm. The apparent depth of a needle lying at the bottom of the tank is measured
by a microscope to be 9.4 cm. What is the refractive index of water? If water is
replaced by a liquid of refractive index 1.63 up to the same height, by what
distance would the microscope have to be moved to focus on the needle again?
Question 9.4 Figures 9.34(a) and (b) show refraction of a ray
in air incident at 60° with the normal to a glass-air and water-air interface,
respectively. Predict the angle of refraction in glass when the angle of
incidence in water is 45º with the normal to a water-glass interface [Fig.
9.34(c)].
Question 9.5 A small bulb is placed at the bottom of a tank
containing water to a depth of 80cm. What is the area of the surface of water
through which light from the bulb can emerge out? Refractive index of water is
1.33. (Consider the bulb to be a point source.)
Question 9.6 A prism is made of glass of unknown refractive
index. A parallel beam of light is incident on a face of the prism. The angle of
minimum deviation is measured to be 40°. What is the refractive index of the
material of the prism? The refracting angle of the prism is 60°. If the prism is
placed in water (refractive index 1.33), predict the new angle of minimum
deviation of a parallel beam of light.
Question 9.7 Double-convex lenses are to be manufactured from
a glass of refractive index 1.55, with both faces of the same radius of
curvature. What is the radius of curvature required if the focal length is to be
20cm?
Question 9.8 A beam of light converges at a point P. Now a
lens is placed in the path of the convergent beam 12cm from P. At what point
does the beam converge if the lens is (a) a convex lens of focal length 20cm,
and (b) a concave lens of focal length 16cm?
Question 9.9 An object of size 3.0cm is placed 14cm in front
of a concave lens of focal length 21cm. Describe the image produced by the lens.
What happens if the object is moved further away from the lens?
Question 9.10 What is the focal length of a convex lens of
focal length 30cm in contact with a concave lens of focal length 20cm?Is the
system a converging or a diverging lens? Ignore thickness of the lenses .
Question 9.11 A compound microscope consists of an objective
lens of focal length 2.0cm and an eyepiece of focal length 6.25cm separated by a
distance of 15cm. How far from the objective should an object be placed in order
to obtain the final image at (a) the least distance of distinct vision (25cm),
and (b) at infinity? What is the magnifying power of the microscope in each
case?
Question 9.12 A person with a normal near point (25cm) using
a compound microscope with objective of focal length 8.0 mm and an eyepiece of
focal length 2.5cm can bring an object placed at 9.0mm from the objective in
sharp focus. What is the separation between the two lenses? Calculate the
magnifying power of the microscope,
Question 9.13 A small telescope has an objective lens of
focal length 144cm and an eyepiece of focal length 6.0cm. What is the magnifying
power of the telescope? What is the separation between the objective and the
eyepiece?
Question 9.14 (a) A giant refracting telescope at an
observatory has an objective lens of focal length 15m. If an eyepiece of focal
length 1.0cm is used, what is the angular magnification of the telescope?
(b) If this telescope is used to view the moon, what is the diameter of the
image of the moon formed by the objective lens? The diameter of the moon is 3.48
× 106m, and the radius of lunar orbit is 3.8 × 108m.
Question 9.15 Use the mirror equation to deduce that:
(a) an object placed between f and 2f of a concave mirror produces a real
image beyond 2f.
(b) a convex mirror always produces a virtual image independent of the location
of the object.
(c) the virtual image produced by a convex mirror is always diminished in size
and is located between the focus and the pole.
(d) an object placed between the pole and focus of a concave mirror produces a
virtual and enlarged image. [Note: This exercise helps you deduce algebraically
properties of images that one obtains from explicit ray diagrams.]
Question 9.16 A small pin fixed on a table top is viewed from
above from a distance of 50cm. By what distance would the pin appear to be
raised if it is viewed from the same point through a 15cm thick glass slab held
parallel to the table? Refractive index of glass = 1.5. Does the answer depend
on the location of the slab?
Question 9.17 (a) Figure 9.35 shows a cross-section of a
‘light pipe’ made of a glass fibre of refractive index 1.68. The outer covering
of the pipe is made of a material of refractive index 1.44. What is the range of
the angles of the incident rays with the axis of the pipe for which total
reflections inside the pipe take place, as shown in the figure.
(b) What is the answer if there is no outer covering of the pipe?
Question 9.18 Answer the following questions:
(a) You have learnt that plane and convex mirrors produce virtual images of
objects. Can they produce real images under some circumstances? Explain.
(b) A virtual image, we always say, cannot be caught on a screen. Yet when we
‘see’ a virtual image, we are obviously bringing it on to the ‘screen’ (i.e.,
the retina) of our eye. Is there a contradiction?
(c) A diver under water, looks obliquely at a fisherman standing on the bank of
a lake. Would the fisherman look taller or shorter to the diver than what he
actually is?
(d) Does the apparent depth of a tank of water change if viewed obliquely? If
so, does the apparent depth increase or decrease?
(e) The refractive index of diamond is much greater than that of ordinary glass.
Is this fact of some use to a diamond cutter?
Question 9.19 The image of a small electric bulb fixed on the
wall of a room is to be obtained on the opposite wall 3m away by means of a
large convex lens. What is the maximum possible focal length of the lens
required for the purpose?
Question 9.20 A screen is placed 90cm from an object. The
image of the object on the screen is formed by a convex lens at two different
locations separated by 20cm. Determine the focal length of the lens.
Question 9.21 (a) Determine the ‘effective focal length’ of
the combination of the two lenses in Exercise 9.10, if they are placed 8.0cm
apart with their principal axes coincident. Does the answer depend on which side
of the combination a beam of parallel light is incident? Is the notion of
effective focal length of this system useful at all?
(b) An object 1.5 cm in size is placed on the side of the convex lens in the
arrangement (a) above. The distance between the object and the convex lens is
40cm. Determine the magnification produced by the two-lens system, and the size
of the image.
Question 9.22 At what angle should a ray of light be incident
on the face of a prism of refracting angle 60° so that it just suffers total
internal reflection at the other face? The refractive index of the material of
the prism is 1.524.
Question 9.23 You are given prisms made of crown glass and
flint glass with a wide variety of angles. Suggest a combination of prisms which
will (a) deviate a pencil of white light without much dispersion, (b) disperse
(and displace) a pencil of white light without much deviation.
Question 9.24 For a normal eye, the far point is at infinity
and the near point of distinct vision is about 25cm in front of the eye. The
cornea of the eye provides a converging power of about 40 dioptres, and the
least converging power of the eye-lens behind the cornea is about 20 dioptres.
From this rough data estimate the range of accommodation (i.e., the range of
converging power of the eye-lens) of a normal eye.
Question 9.25 Does short-sightedness (myopia) or
long-sightedness (hypermetropia) imply necessarily that the eye has partially
lost its ability of accommodation? If not, what might cause these defects of
vision?
Question 9.26 A myopic person has been using spectacles of
power –1.0 dioptre for distant vision. During old age he also needs to use
separate reading glass of power + 2.0 dioptres. Explain what may have happened.
Question 9.27 A person looking at a person wearing a shirt
with a pattern comprising vertical and horizontal lines is able to see the
vertical lines more distinctly than the horizontal ones. What is this defect due
to? How is such a defect of vision corrected?
Question 9.28 A man with normal near point (25 cm) reads a
book with small print using a magnifying glass: a thin convex lens of focal
length 5 cm.
(a) What is the closest and the farthest distance at which he should keep
the lens from the page so that he can read the book when viewing through the
magnifying glass?
(b) What is the maximum and the minimum angular magnification (magnifying power)
possible using the above simple microscope?
Question 9.29 A card sheet divided into squares each of
size 1 mm2 is being viewed at a distance of 9 cm through a magnifying glass (a
converging lens of focal length 9 cm) held close to the eye.
(a) What is the magnification produced by the lens? How much is the area of
each square in the virtual image?
(b) What is the angular magnification (magnifying power) of the lens?
(c) Is the magnification in
(a) equal to the magnifying power in (b)? Explain.
Question 9.30 (a) At what distance should the lens be held
from the figure in Exercise 9.29 in order to view the squares distinctly with
the maximum possible magnifying power?
(b) What is the magnification in this case?
(c) Is the magnification equal to the magnifying power in this case? Explain.
9.31 What should be the distance between the object in Exercise
Question 9.30 and the magnifying glass if the virtual image
of each square in the figure is to have an area of 6.25 mm2. Would you be able
to see the squares distinctly with your eyes very close to the magnifier?
[Note: Exercises 9.29 to
Question 9.31will help you clearly understand the tion (or
magnifying power) of an instrument.]
Question 9.32 Answer the following questions:
(a) The angle subtended at the eye by an object is equal to the angle
subtended at the eye by the virtual image produced by a magnifying glass. In
what sense then does a magnifying glass provide angular magnification?
(b) In viewing through a magnifying glass, one usually positions one’s eyes very
close to the lens. Does angular magnification change if the eye is moved back?
(c) Magnifying power of a simple microscope is inversely proportional to the
focal length of the lens. What then stops us from using a convex lens of smaller
and smaller focal length and achieving greater and greater magnifying power? (d)
Why must both the objective and the eyepiece of a compound microscope have short
focal lengths?
(e) When viewing through a compound microscope, our eyes should be positioned
not on the eyepiece but a short distance away from it for best viewing. Why? How
much should be that short distance between the eye and eyepiece?
Question 9.33 An angular magnification (magnifying power) of
30X is desired using an objective of focal length 1.25cm and an eyepiece of
focal length 5cm. How will you set up the compound microscope?
Question 9.34 A small telescope has an objective lens of
focal length 140cm and an eyepiece of focal length 5.0cm.
What is the magnifying power of the telescope for viewing distant objects
when
(a) the telescope is in normal adjustment (i.e., when the final image is at
infinity)?
(b) the final image is formed at the least distance of distinct vision (25cm)?
Question 9.35 (a) For the telescope described in Exercise 3.4
(a), what is the separation between the objective lens and the eyepiece? (b) If
this telescope is used to view a 100 m tall tower 3 km away, what is the height
of the image of the tower formed by the objective lens? (c) What is the height
of the final image of the tower if it is formed at 25cm?
Question 9.36 A Cassegrain telescope uses two mirrors as
shown in Fig. 9.33. Such a telescope is built with the mirrors 20mm apart. If
the radius of curvature of the large mirror is 220mm and the small mirror is
140mm, where will the final image of an object at infinity be?
Question 9.37 Light incident normally on a plane mirror
attached to a galvanometer coil retraces backwards as shown in Fig.
Question 9.36. A current in the coil produces a deflection of
3.5o of the mirror. What is the displacement of the reflected spot of light on a
screen placed 1.5 m away?
Question 9.39 shows an equiconvex lens (of refractive index
1.50) in contact with a liquid layer on top of a plane mirror. A small needle
with its tip on the principal axis is moved along the axis until its inverted
image is found at the position of the needle. The distance of the needle from
the lens is measured to be 45.0cm. The liquid is removed and the experiment is
repeated. The new distance is measured to be 30.0cm. What is the refractive
index of the liquid?
:: Chapter 10 - Wave Optics ::
Question 10.1 Monochromatic light of wavelength 589 nm is
incident from air on a water surface. What are the wavelength, frequency and
speed of (a) reflected, and (b) refracted light? Refractive index of water is
1.33.
Question 10.2 What is the shape of the wavefront in each of the following
cases:
(a) Light diverging from a point source.
(b) Light emerging out of a convex lens when a point source is placed at its
focus.
(c) The portion of the wavefront of light from a distant star intercepted by the
Earth.
Question 10.3 (a) The refractive index of glass is 1.5. What
is the speed of light in glass? (Speed of light in vacuum is 3.0 × 108 m s–1)
(b) Is the speed of light in glass independent of the colour of light? If not,
which of the two colours red and violet travels slower in a glass prism?
Question 10.4 In a Young’s double-slit experiment, the slits
are separated by 0.28 mm and the screen is placed 1.4 m away. The distance
between the central bright fringe and the fourth bright fringe is measured to be
1.2 cm. Determine the wavelength of light used in the experiment.
Question 10.5 In Young’s double-slit experiment using
monochromatic light of wavelength λ, the intensity of light at a point on the
screen where path difference is λ, is K units. What is the intensity of light at
a point where path difference is λ/3?
Question 10.6 A beam of light consisting of two
wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a
Young’s double-slit experiment.
(a) Find the distance of the third bright fringe on the screen from the
central maximum for wavelength 650 nm.
(b) What is the least distance from the central maximum where the bright fringes
due to both the wavelengths coincide?
Question 10.7 In a double-slit experiment the angular width
of a fringe is found to be 0.2° on a screen placed 1 m away. The wavelength of
light used is 600 nm. What will be the angular width of the fringe if the entire
experimental apparatus is immersed in water? Take refractive index of water to
be 4/3.
Question 10.8 What is the Brewster angle for air to glass
transition? (Refractive index of glass = 1.5.)
Question 10.9 Light of wavelength 5000 Å falls on a plane
reflecting surface. What are the wavelength and frequency of the reflected
light? For what angle of incidence is the reflected ray normal to the incident
ray?
Question 10.10 Estimate the distance for which ray optics is
good approximation for an aperture of 4 mm and wavelength 400 nm.
ADDITIONAL EXERCISES QUESTIONS
Question 10.11 The 6563 Å Hα line emitted by hydrogen in a
star is found to be redshifted by 15 Å. Estimate the speed with which the star
is receding from the Earth.
Question 10.12 Explain how Corpuscular theory predicts the
speed of light in a medium, say, water, to be greater than the speed of light in
vacuum. Is the prediction confirmed by experimental determination of the speed
of light in water? If not, which alternative picture of light is consistent with
experiment?
Question 10.13 You have learnt in the text how Huygens’
principle leads to the laws of reflection and refraction. Use the same principle
to deduce directly that a point object placed in front of a plane mirror
produces a virtual image whose distance from the mirror is equal to the object
distance from the mirror.
Question 10.14 Let us list some of the factors, which
could possibly influence the speed of wave propagation:
(i) nature of the source.
(ii) direction of propagation.
(iii) motion of the source and/or observer.
(iv) wavelength.
(v) intensity of the wave. On which of these factors, if any, does (a) the speed
of light in vacuum, (b) the speed of light in a medium (say, glass or water),
depend?
Question 10.15 For sound waves, the Doppler formula for
frequency shift differs slightly between the two situations:
(i) source at rest; observer moving, and (ii) source moving; observer at
rest. The exact Doppler formulas for the case of light waves in vacuum are,
however, strictly identical for these situations. Explain why this should be so.
Would you expect the formulas to be strictly identical for the two situations in
case of light travelling in a medium?
Question 10.16 In double-slit experiment using light of
wavelength 600 nm, the angular width of a fringe formed on a distant screen is
0.1º. What is the spacing between the two slits?
Question 10.17 Answer the following questions:
(a) In a single slit diffraction experiment, the width of the slit is made
double the original width. How does this affect the size and intensity of the
central diffraction band?
(b) In what way is diffraction from each slit related to the interference
pattern in a double-slit experiment?
(c) When a tiny circular obstacle is placed in the path of light from a distant
source, a bright spot is seen at the centre of the shadow of the obstacle.
Explain why?
(d) Two students are separated by a 7 m partition wall in a room 10 m high. If
both light and sound waves can bend around obstacles, how is it that the
students are unable to see each other even though they can converse easily.
(e) Ray optics is based on the assumption that light travels in a straight line.
Diffraction effects (observed when light propagates through small
apertures/slits or around small obstacles) disprove this assumption. Yet the ray
optics assumption is so commonly used in understanding location and several
other properties of images in optical instruments. What is the justification?
Question 10.18 Two towers on top of two hills are 40 km
apart. The line joining them passes 50 m above a hill halfway between the
towers. What is the longest wavelength of radio waves, which can be sent between
the towers without appreciable diffraction effects?
Question 10.19 A parallel beam of light of wavelength 500 nm
falls on a narrow slit and the resulting diffraction pattern is observed on a
screen 1 m away. It is observed that the first minimum is at a distance of 2.5
mm from the centre of the screen. Find the width of the slit.
Question 10.20 Answer the following questions:
(a) When a low flying aircraft passes overhead, we sometimes notice a slight
shaking of the picture on our TV screen. Suggest a possible explanation.
(b) As you have learnt in the text, the principle of linear superposition of
wave displacement is basic to understanding intensity distributions in
diffraction and interference patterns. What is the justification of this
principle?
Question 10.21 In deriving the single slit diffraction
pattern, it was stated that the intensity is zero at angles of nλ/a. Justify
this by suitably dividing the slit to bring out the cancellation.
:: Chapter 11 - Dual nature of Radiation and Matter ::
Question 11.1 Find the (a) maximum frequency, and (b) minimum
wavelength of X-rays produced by 30 kV electrons.
Question 11.2 The work function of caesium metal is 2.14 eV.
When light of frequency 6 ×1014Hz is incident on the metal surface,
photoemission of electrons occurs. What is the (a) maximum kinetic energy of the
emitted electrons, (b) Stopping potential, and (c) maximum speed of the emitted
photoelectrons?
Question 11.3 The photoelectric cut-off voltage in a certain
experiment is 1.5 V. What is the maximum kinetic energy of photoelectrons
emitted?
Question 11.4 Monochromatic light of wavelength 632.8 nm is
produced by a helium-neon laser. The power emitted is 9.42 mW. (a) Find the
energy and momentum of each photon in the light beam, (b) How many photons per
second, on the average, arrive at a target irradiated by this beam? (Assume the
beam to have uniform cross-section which is less than the target area), and (c)
How fast does a hydrogen atom have to travel in order to have the same momentum
as that of the photon?
Question 11.5 The energy flux of sunlight reaching the
surface of the earth is 1.388 × 103 W/m2. How many photons (nearly) per square
metre are incident on the Earth per second? Assume that the photons in the
sunlight have an average wavelength of 550 nm.
Question 11.6 In an experiment on photoelectric effect, the
slope of the cut-off voltage versus frequency of incident light is found to be
4.12 × 10–15 V s. Calculate the value of Planck’s constant.
Question 11.7 A 100W sodium lamp radiates energy uniformly in
all directions. The lamp is located at the centre of a large sphere that absorbs
all the sodium light which is incident on it. The wavelength of the sodium light
is 589 nm. (a) What is the energy per photon associated with the sodium light?
(b) At what rate are the photons delivered to the sphere?
Question 11.8 The threshold frequency for a certain metal is
3.3 × 1014 Hz. If light of frequency 8.2 × 1014 Hz is incident on the metal,
predict the cutoff voltage for the photoelectric emission.
Question 11.9 The work function for a certain metal is 4.2 eV.
Will this metal give photoelectric emission for incident radiation of wavelength
330 nm?
Question 11.10 Light of frequency 7.21 × 1014 Hz is incident
on a metal surface. Electrons with a maximum speed of 6.0 × 105 m/s are ejected
from the surface. What is the threshold frequency for photoemission of
electrons?
Question 11.11 Light of wavelength 488 nm is produced by an
argon laser which is used in the photoelectric effect. When light from this
spectral line is incident on the emitter, the stopping (cut-off) potential of
photoelectrons is 0.38 V. Find the work function of the material from which the
emitter is made.
Question 11.12 Calculate the (a) momentum, and (b) de Broglie
wavelength of the electrons accelerated through a potential difference of 56V.
Question 11.13 What is the (a) momentum, (b) speed, and (c)
de Broglie wavelength of an electron with kinetic energy of 120 eV.
Question 11.14 The wavelength of light from the spectral
emission line of sodium is 589 nm. Find the kinetic energy at which (a) an
electron, and (b) a neutron, would have the same de Broglie wavelength.
Question 11.15 What is the de Broglie wavelength of (a) a bullet of mass 0.040
kg travelling at the speed of 1.0 km/s, (b) a ball of mass 0.060 kg moving at a
speed of 1.0 m/s, and (c) a dust particle of mass 1.0 × 10–9 kg drifting with a
speed of 2.2 m/s?
Question 11.16 An electron and a photon each have a wavelength of 1.00 nm. Find
(a) their momenta, (b) the energy of the photon, and (c) the kinetic energy of
electron.
Question 11.17 (a) For what kinetic energy of a neutron will the associated de
Broglie wavelength be 1.40 × 10–10m? (b) Also find the de Broglie wavelength of
a neutron, in thermal equilibrium with matter, having an average kinetic energy
of (3/2) k T at 300 K.
Question 11.18 Show that the wavelength of electromagnetic
radiation is equal to the de Broglie wavelength of its quantum (photon).
Question 11.19 What is the de Broglie wavelength of a
nitrogen molecule in air at 300 K? Assume that the molecule is moving with the
root-meansquare speed of molecules at this temperature. (Atomic mass of nitrogen
= 14.0076 u)
ADDITIONAL EXERCISES QUESTIONS
Question 11.20 (a) Estimate the speed with which electrons
emitted from a heated emitter of an evacuated tube impinge on the collector
maintained at a potential difference of 500 V with respect to the emitter.
Ignore the small initial speeds of the electrons. The specific charge of the
electron, i.e., its e/m is given to be 1.76 × 1011 C kg–1. (b) Use the same
formula you employ in (a) to obtain electron speed for an collector potential of
10 MV. Do you see what is wrong ? In what way is the formula to be modified?
Question 11.21 (a) A monoenergetic electron beam with
electron speed of 5.20 × 106 m s–1 is subject to a magnetic field of 1.30 × 10–4
T normal to the beam velocity. What is the radius of the circle traced by the
beam, given e/m for electron equals 1.76 × 1011C kg–1. (b) Is the formula you
employ in (a) valid for calculating radius of the path of a 20 MeV electron
beam? If not, in what way is it modified ? [Note: Exercises 11.20(b) and 11.21
(b) take you to relativistic mechanics which is beyond the scope of this book.
They have been inserted here simply to emphasise the point that the formulas you
use in part (a) of the exercises are not valid at very high speeds or energies.
See answers at the end to know what ‘very high speed or energy’ means.
Question 11.22 An electron gun with its collector at a
potential of 100 V fires out electrons in a spherical bulb containing hydrogen
gas at low pressure (∼10–2 mm of Hg). A magnetic field of 2.83 × 10–4 T curves
the path of the electrons in a circular orbit of radius 12.0 cm. (The path can
be viewed because the gas ions in the path focus the beam by attracting
electrons, and emitting light by electron capture; this method is known as the
‘fine beam tube’ method.) Determine e/m from the data.
Question 11.23 (a) An X-ray tube produces a continuous
spectrum of radiation with its short wavelength end at 0.45 Å. What is the
maximum energy of a photon in the radiation? (b) From your answer to (a), guess
what order of accelerating voltage (for electrons) is required in such a tube?
Question 11.24 In an accelerator experiment on high-energy
collisions of electrons with positrons, a certain event is interpreted as
annihilation of an electron-positron pair of total energy 10.2 BeV into two
γ-rays of equal energy. What is the wavelength associated with each γ-ray? (1BeV
= 109 eV)
Question 11.25 Estimating the following two numbers should be
interesting. The first number will tell you why radio engineers do not need to
worry much about photons! The second number tells you why our eye can never
‘count photons’, even in barely detectable light. (a) The number of photons
emitted per second by a Medium wave transmitter of 10 kW power, emitting
radiowaves of wavelength 500 m.
(b) The number of photons entering the pupil of our eye per second corresponding
to the minimum intensity of white light that we humans can perceive (∼10–10 W
m–2). Take the area of the pupil to be about 0.4 cm2, and the average frequency
of white light to be about 6 × 1014 Hz.
Question 11.26 Ultraviolet light of wavelength 2271 Å from a
100 W mercury source irradiates a photo-cell made of molybdenum metal. If the
stopping potential is –1.3 V, estimate the work function of the metal. How would
the photo-cell respond to a high intensity (∼105 W m–2) red light of wavelength
6328 Å produced by a He-Ne laser?
Question 11.27 Monochromatic radiation of wavelength 640.2 nm
(1nm = 10–9 m) from a neon lamp irradiates photosensitive material made of
caesium on tungsten. The stopping voltage is measured to be 0.54 V. The source
is replaced by an iron source and its 427.2 nm line irradiates the same
photo-cell. Predict the new stopping voltage.
Question 11.28 A mercury lamp is a convenient source for
studying frequency dependence of photoelectric emission, since it gives a number
of spectral lines ranging from the UV to the red end of the visible spectrum. In
our experiment with rubidium photo-cell, the following lines from a mercury
source were used: λ1 = 3650 Å, λ2= 4047 Å, λ3= 4358 Å, λ4= 5461 Å, λ5= 6907 Å,
The stopping voltages, respectively, were measured to be: V01 = 1.28 V, V02 =
0.95 V, V03 = 0.74 V, V04 = 0.16 V, V05 = 0 V Determine the value of Planck’s
constant h, the threshold frequency and work function for the material. [Note:
You will notice that to get h from the data, you will need to know e (which you
can take to be 1.6 × 10–19 C). Experiments of this kind on Na, Li, K, etc. were
performed by Millikan, who, using his own value of e (from the oil-drop
experiment) confirmed Einstein’s photoelectric equation and at the same time
gave an independent estimate of the value of h.
Question 11.29 The work function for the following metals is
given: Na: 2.75 eV; K: 2.30 eV; Mo: 4.17 eV; Ni: 5.15 eV. Which of these metals
will not give photoelectric emission for a radiation of wavelength 3300 Å from a
He-Cd laser placed 1 m away from the photocell? What happens if the laser is
brought nearer and placed 50 cm away?
Question 11.30 Light of intensity 10–5 W m–2 falls on a
sodium photo-cell of surface area 2 cm2. Assuming that the top 5 layers of
sodium absorb the incident energy, estimate time required for photoelectric
emission in the wave-picture of radiation. The work function for the metal is
given to be about 2 eV. What is the implication of your answer?
Question 11.31 Crystal diffraction experiments can be
performed using X-rays, or electrons accelerated through appropriate voltage.
Which probe has greater energy? (For quantitative comparison, take the
wavelength of the probe equal to 1 Å, which is of the order of inter-atomic
spacing in the lattice) (me=9.11 × 10–31 kg).
11.32 (a) Obtain the de Broglie wavelength of a neutron of
kinetic energy 150 eV. As you have seen in Exercise
Question 11.31, an electron beam of this energy is suitable
for crystal diffraction experiments. Would a neutron beam of the same energy be
equally suitable ? Explain. (mn = 1.675 × 10–27 kg) (b) Obtain the de Broglie
wavelength associated with thermal neutrons at room temperature (27 ºC). Hence
explain why a fast neutron beam needs to be thermalised with the environment
before it can be used for neutron diffraction experiments.
Question 11.33 An electron microscope uses electrons
accelerated by a voltage of 50 kV. Determine the de Broglie wavelength
associated with the electrons. If other factors (such as numerical aperture,
etc.) are taken to be roughly the same, how does the resolving power of an
electron microscope compare with that of an optical microscope which uses yellow
light?
Question 11.34 The wavelength of a probe is roughly a measure
of the size of a structure that it can probe in some detail. The quark structure
of protons and neutrons appears at the minute length-scale of 10–15 m or less.
This structure was first probed in early 1970’s using high energy electron beams
produced by a linear accelerator at Stanford, USA. Guess what might have been
the order of energy of these electron beams. (Rest mass energy of electron =
0.511 MeV.)
Question 11.35 Find the typical de Broglie wavelength
associated with a He atom in helium gas at room temperature (27 ºC) and 1 atm
pressure; and compare it with the mean separation between two atoms under these
conditions.
Question 11.36 Compute the typical de Broglie wavelength of
an electron in a metal at 27 ºC and compare it with the mean separation between
two electrons in a metal which is given to be about 2 × 10–10 m. [Note:
Exercises 11.35 and 11.36 reveal that while the wave-packets
associated with gaseous molecules under ordinary conditions are non-overlapping,
the electron wave-packets in a metal strongly overlap with one another. This
suggests that whereas molecules in an ordinary gas can be distinguished apart,
electrons in a metal cannot be distintguished apart from one another. This
indistinguishibility has many fundamental implications which you will explore in
more advanced Physics courses.]
Question 11.37 Answer the following questions:
(a) Quarks inside protons and neutrons are thought to carry
fractional charges [(+2/3)e ; (–1/3)e]. Why do they not show up in Millikan’s
oil-drop experiment?
(b) What is so special about the combination e/m? Why do we not simply talk of e
and m separately?
(c) Why should gases be insulators at ordinary pressures and start conducting at
very low pressures?
(d) Every metal has a definite work function. Why do all photoelectrons not come
out with the same energy if incident radiation is monochromatic? Why is there an
energy distribution of photoelectrons?
(e) The energy and momentum of an electron are related to the frequency and
wavelength of the associated matter wave by the relations: E = h ν, p = λ h But
while the value of λ is physically significant, the value of ν (and therefore,
the value of the phase speed ν λ) has no physical significance. Why?
:: Chapter 12 - Atoms ::
Question 12.1 Choose the correct alternative from the
clues given at the end of the each statement:
(a) The size of the atom in Thomson’s model is .......... the
atomic size in Rutherford’s model. (much greater than/no different from/much
less than.)
(b) In the ground state of .......... electrons are in stable equilibrium, while
in .......... electrons always experience a net force. (Thomson’s model/
Rutherford’s model.)
(c) A classical atom based on .......... is doomed to collapse. (Thomson’s
model/ Rutherford’s model.)
(d) An atom has a nearly continuous mass distribution in a .......... but has a
highly non-uniform mass distribution in .......... (Thomson’s model/
Rutherford’s model.)
(e) The positively charged part of the atom possesses most of the mass in
.......... (Rutherford’s model/both the models.)
Question 12.2 Suppose you are given a chance to repeat the
alpha-particle scattering experiment using a thin sheet of solid hydrogen in
place of the gold foil. (Hydrogen is a solid at temperatures below 14 K.) What
results do you expect?
Question 12.3 What is the shortest wavelength present in the
Paschen series of spectral lines?
Question 12.4 A difference of 2.3 eV separates two energy
levels in an atom. What is the frequency of radiation emitted when the atom make
a transition from the upper level to the lower level?
Question 12.5 The ground state energy of hydrogen atom is
–13.6 eV. What are the kinetic and potential energies of the electron in this
state?
Question 12.6 A hydrogen atom initially in the ground level
absorbs a photon, which excites it to the n = 4 level. Determine the wavelength
and frequency of photon.
Question 12.7 (a) Using the Bohr’s model calculate the speed
of the electron in a hydrogen atom in the n = 1, 2, and 3 levels. (b) Calculate
the orbital period in each of these levels.
Question 12.8 The radius of the innermost electron orbit of a
hydrogen atom is 5.3×10–11 m. What are the radii of the n = 2 and n =3 orbits?
Question 12.9 A12.5 eV electron beam is used to bombard
gaseous hydrogen at room temperature. What series of wavelengths will be
emitted?
Question 12.10 In accordance with the Bohr’s model, find the
quantum number that characterises the earth’s revolution around the sun in an
orbit of radius 1.5 × 1011 m with orbital speed 3 × 104 m/s. (Mass of earth =
6.0 × 1024 kg.)
ADDITIONAL EXERCISES QUESTIONS
Question 12.11 Answer the following questions, which help
you understand the difference between Thomson’s model and Rutherford’s model
better.
(a) Is the average angle of deflection of α-particles by a
thin gold foil predicted by Thomson’s model much less, about the same, or much
greater than that predicted by Rutherford’s model?
(b) Is the probability of backward scattering (i.e., scattering of α-particles
at angles greater than 90°) predicted by Thomson’s model much less, about the
same, or much greater than that predicted by Rutherford’s model?
(c) Keeping other factors fixed, it is found experimentally that for small
thickness t, the number of α-particles scattered at moderate angles is
proportional to t. What clue does this linear dependence on t provide?
(d) In which model is it completely wrong to ignore multiple scattering for the
calculation of average angle of scattering of α-particles by a thin foil?
Question 12.12 The gravitational attraction between electron
and proton in a hydrogen atom is weaker than the coulomb attraction by a factor
of about 10–40. An alternative way of looking at this fact is to estimate the
radius of the first Bohr orbit of a hydrogen atom if the electron and proton
were bound by gravitational attraction. You will find the answer interesting.
Question 12.13 Obtain an expression for the frequency of
radiation emitted when a hydrogen atom de-excites from level n to level (n–1).
For large n, show that this frequency equals the classical frequency of
revolution of the electron in the orbit.
Question 12.14 Classically, an electron can be in any
orbit around the nucleus of an atom. Then what determines the typical atomic
size? Why is an atom not, say, thousand times bigger than its typical size? The
question had greatly puzzled Bohr before he arrived at his famous model of the
atom that you have learnt in the text. To simulate what he might well have done
before his discovery, let us play as follows with the basic constants of nature
and see if we can get a quantity with the dimensions of length that is roughly
equal to the known size of an atom (~ 10–10m).
(a) Construct a quantity with the dimensions of length from
the fundamental constants e, me, and c. Determine its numerical value.
(b) You will find that the length obtained in (a) is many orders of magnitude
smaller than the atomic dimensions. Further, it involves c. But energies of
atoms are mostly in non-relativistic domain where c is not expected to play any
role. This is what may have suggested Bohr to discard c and look for ‘something
else’ to get the right atomic size. Now, the Planck’s constant h had already
made its appearance elsewhere. Bohr’s great insight lay in recognising that h,
me, and e will yield the right atomic size. Construct a quantity with the
dimension of length from h, me, and e and confirm that its numerical value has
indeed the correct order of magnitude.
Question 12.15 The total energy of an electron in the
first excited state of the hydrogen atom is about –3.4 eV.
(a) What is the kinetic energy of the electron in this state?
(b) What is the potential energy of the electron in this state?
(c) Which of the answers above would change if the choice of the zero of
potential energy is changed?
Question 12.16 If Bohr’s quantisation postulate (angular
momentum = nh/2π) is a basic law of nature, it should be equally valid for the
case of planetary motion also. Why then do we never speak of quantisation of
orbits of planets around the sun?
Question 12.17 Obtain the first Bohr’s radius and the ground
state energy of a muonic hydrogen atom [i.e., an atom in which a negatively
charged muon (μ–) of mass about 207me orbits around a proton].
:: Chapter 13 - Nuclei ::
Question 13.1 (a) Two stable isotopes of lithium 6 3 Li and 7
3 Li have respective abundances of 7.5% and 92.5%. These isotopes have masses
6.01512 u and 7.01600 u, respectively. Find the atomic mass of lithium.
(b) Boron has two stable isotopes, 10 5B and 11 5B. Their respective masses are
10.01294 u and 11.00931 u, and the atomic mass of boron is 10.811 u. Find the
abundances of 10 5B and 11 5 B .
Question 13.2 The three stable isotopes of neon: 20 21 22 10
10 10 Ne, Ne and Ne have respective abundances of 90.51%, 0.27% and 9.22%. The
atomic masses of the three isotopes are 19.99 u, 20.99 u and 21.99 u,
respectively. Obtain the average atomic mass of neon.
Question 13.3 Obtain the binding energy (in MeV) of a
nitrogen nucleus (14 ) 7N , given m (14 ) 7N =14.00307 u
Question 13.4 Obtain the binding energy of the nuclei 56 26Fe
and 209 83 Bi in units of MeV from the following data:
m ( 56 26Fe ) = 55.934939 u m ( 209 83 Bi ) = 208.980388 u
Question 13.5 A given coin has a mass of 3.0 g. Calculate the
nuclear energy that would be required to separate all the neutrons and protons
from each other. For simplicity assume that the coin is entirely made of 63 29Cu
atoms (of mass 62.92960 u).
Question 13.6 Write nuclear reaction equations for (i)
α-decay of 226 88 Ra (ii) α-decay of 242 94 Pu (iii) β–-decay of 32 15 P (iv)
β–-decay of 210 83 Bi (v) β+-decay of 11 6 C (vi) β+-decay of 97 43 Tc (vii)
Electron capture of 120 54 Xe
Question 13.7 A radioactive isotope has a half-life of T
years. How long will it take the activity to reduce to a) 3.125%, b) 1% of its
original value?
Question 13.8 The normal activity of living carbon-containing
matter is found to be about 15 decays per minute for every gram of carbon. This
activity arises from the small proportion of radioactive 14 6C present with the
stable carbon isotope 12 6C . When the organism is dead, its interaction with
the atmosphere (which maintains the above equilibrium activity) ceases and its
activity begins to drop. From the known half-life (5730 years) of 14 6C , and
the measured activity, the age of the specimen can be approximately estimated.
This is the principle of 14 6C dating used in archaeology. Suppose a specimen
from Mohenjodaro gives an activity of 9 decays per minute per gram of carbon.
Estimate the approximate age of the Indus-Valley civilisation.
Question 13.9 Obtain the amount of 60 27Co necessary to
provide a radioactive source of 8.0 mCi strength. The half-life of 60 27Co is
5.3 years.
Question 13.10 The half-life of 90 38Sr is 28 years. What is
the disintegration rate of 15 mg of this isotope?
Question 13.11 Obtain approximately the ratio of the nuclear
radii of the gold isotope 197 79 Au and the silver isotope 107 47 Ag .
Question 13.12 Find the Q-value and the kinetic energy of the
emitted α-particle in the α-decay of (a) 226 88 Ra and (b) 220 86 Rn . Given m (
226 88 Ra ) = 226.02540 u, m ( 222 86 Rn ) = 222.01750 u, m ( 222 86 Rn ) =
220.01137 u, m ( 216 84 Po ) = 216.00189 u.
Question 13.13 The radionuclide 11C decays according to 11 11
+ 6C → 5 B+e +ν : T1/2=20.3 min The maximum energy of the emitted positron is
0.960 MeV. Given the mass values: m ( 11 6C) = 11.011434 u and m ( 11 6B ) =
11.009305 u, calculate Q and compare it with the maximum energy of the positron
emitted.
Question 13.14 The nucleus 23 10 Ne decays by β– emission.
Write down the β-decay equation and determine the maximum kinetic energy of the
electrons emitted. Given that: m ( 23 10 Ne ) = 22.994466 u m ( 23 11 Na ) =
22.089770 u.
Question 13.15 The Q value of a nuclear reaction A + b → C +
d is defined by Q = [ mA + mb – mC – md]c2 where the masses refer to the
respective nuclei. Determine from the given data the Q-value of the following
reactions and state whether the reactions are exothermic or endothermic. (i) 1 3
2 2 1 1 1 1 H+ H → H+ H (ii) 12 12 20 4 6 6 10 2 C+ C → Ne+ He Atomic masses are
given to be m ( 2 1H) = 2.014102 u m ( 3 1H) = 3.016049 u m ( 12 6C ) =
12.000000 u m ( 20 10 Ne ) = 19.992439 u
Question 13.16 Suppose, we think of fission of a 56 26Fe
nucleus into two equal fragments, 28 13 Al . Is the fission energetically
possible? Argue by working out Q of the process. Given m ( 56 26Fe ) = 55.93494
u and m ( 28 13 Al ) = 27.98191 u.
Question 13.17 The fission properties of 239 94 Pu are very
similar to those of 235 92 U. The average energy released per fission is 180 MeV.
How much energy, in MeV, is released if all the atoms in 1 kg of pure 239 94 Pu
undergo fission?
Question 13.18 A 1000 MW fission reactor consumes half of its
fuel in 5.00 y. How much 235 92 U did it contain initially? Assume that the
reactor operates 80% of the time, that all the energy generated arises from the
fission of 235 92 U and that this nuclide is consumed only by the fission
process.
Question 13.19 How long can an electric lamp of 100W be kept
glowing by fusion of 2.0 kg of deuterium? Take the fusion reaction as 2 2 3 1H+
1H→ 2He+n+3.27 MeV?
Question 13.20 Calculate the height of the potential barrier
for a head on collision of two deuterons. (Hint: The height of the potential
barrier is given by the Coulomb repulsion between the two deuterons when they
just touch each other. Assume that they can be taken as hard spheres of radius
2.0 fm.)
Question 13.21 From the relation R = R0A1/3, where R0 is a
constant and A is the mass number of a nucleus, show that the nuclear matter
density is nearly constant (i.e. independent of A).
Question 13.22 For the β+ (positron) emission from a nucleus,
there is another competing process known as electron capture (electron from an
inner orbit, say, the K–shell, is captured by the nucleus and a neutrino is
emitted). 1 A A Z Z e+ X Y ν − + → + Show that if β+ emission is energetically
allowed, electron capture is necessarily allowed but not vice–versa.
ADDITIONAL EXERCISES QUESTIONS
Question 13.23 In a periodic table the average atomic mass of
magnesium is given as 24.312 u. The average value is based on their relative
natural abundance on earth. The three isotopes and their masses are 24 12Mg
(23.98504u), 25 12Mg (24.98584u) and 26 12Mg (25.98259u). The natural abundance
of 24 12Mg is 78.99% by mass. Calculate the abundances of other two isotopes.
Question 13.24 The neutron separation energy is defined as
the energy required to remove a neutron from the nucleus. Obtain the neutron
separation energies of the nuclei 41 20Ca and 27 13 Al from the following data:
m( 40 20Ca ) = 39.962591 u m( 41 20Ca ) = 40.962278 u m( 26 13 Al ) = 25.986895
u m( 27 13 Al ) = 26.981541 u?
Question 13.25 A source contains two phosphorous radio
nuclides 32 15P (T1/2 = 14.3d) and 33 15P (T1/2 = 25.3d). Initially, 10% of the
decays come from 33 15P . How long one must wait until 90% do so?
Question 13.26 Under certain circumstances, a nucleus can
decay by emitting a particle more massive than an α-particle. Consider the
following decay processes: 223 209 14 88 82 6 Ra→ Pb + C 223 219 4 88Ra→ 86Rn +
2He Calculate the Q-values for these decays and determine that both are
energetically allowed.
Question 13.27 Consider the fission of 238 92U by fast
neutrons. In one fission event, no neutrons are emitted and the final end
products, after the beta decay of the primary fragments, are 140 58Ce and 99
44Ru . Calculate Q for this fission process. The relevant atomic and particle
masses are m( 238 92U ) =238.05079 u m( 140 58Ce ) =139.90543 u m( 99 44Ru ) =
98.90594 u
Question 13.28 Consider the D–T reaction (deuterium–tritium
fusion) 2 3 4 1 1 2 H+ H→ He + n (a) Calculate the energy released in MeV in
this reaction from the data: m( 2 1H )=2.014102 u m( 3 1H ) =3.016049 u (b)
Consider the radius of both deuterium and tritium to be approximately 2.0 fm.
What is the kinetic energy needed to overcome the coulomb repulsion between the
two nuclei? To what temperature must the gas be heated to initiate the reaction?
(Hint: Kinetic energy required for one fusion event =average thermal kinetic
energy available with the interacting particles = 2(3kT/2); k = Boltzman’s
constant, T = absolute temperature.)
Question 13.29 Obtain the maximum kinetic energy of
β-particles, and the radiation frequencies of γ decays in the decay scheme shown
in Fig. 13.6. You are given that m(198Au) = 197.968233 u m(198Hg) =197.966760 u
Question 13.30 Calculate and compare the energy released by
a) fusion of 1.0 kg of hydrogen deep within Sun and b) the fission of 1.0 kg of
235U in a fission reactor.
Question 13.31 Suppose India had a target of producing by
2020 AD, 200,000 MW of electric power, ten percent of which was to be obtained
from nuclear power plants. Suppose we are given that, on an average, the
efficiency of utilization (i.e. conversion to electric energy) of thermal energy
produced in a reactor was 25%. How much amount of fissionable uranium would our
country need per year by 2020? Take the heat energy per fission of 235U to be
about 200MeV.
:: Chapter 14 - Semiconductor Electronics: Materials, Devices
and Simple Circuits ::
Question 14.1 In an n-type silicon, which of the following
statement is true:
(a) Electrons are majority carriers and trivalent atoms are the dopants.
(b) Electrons are minority carriers and pentavalent atoms are the dopants.
(c) Holes are minority carriers and pentavalent atoms are the dopants.
(d) Holes are majority carriers and trivalent atoms are the dopants.
Question 14.2 Which of the statements given in Exercise 14.1
is true for p-type semiconductos.
Question 14.3 Carbon, silicon and germanium have four valence
electrons each. These are characterised by valence and conduction bands
separated by energy band gap respectively equal to (Eg)C, (Eg)Si and (Eg)Ge.
Which of the following statements is true?
(a) (Eg)Si < (Eg)Ge < (Eg)C (b) (Eg)C < (Eg)Ge > (Eg)Si (c) (Eg)C
> (Eg)Si > (Eg)Ge (d) (Eg)C = (Eg)Si = (Eg)Ge
Question 14.4 In an unbiased p-n junction, holes diffuse
from the p-region to n-region because
(a) free electrons in the n-region attract them.
(b) they move across the junction by the potential difference .
(c) hole concentration in p-region is more as compared to n-region.
(d) All the above.
Question 14.5 When a forward bias is applied to a p-n
junction, it (a) raises the potential barrier.
(b) reduces the majority carrier current to zero.
(c) lowers the potential barrier.
(d) None of the above.
Question 14.6 For transistor action, which of the
following statements are correct:
(a) Base, emitter and collector regions should have similar size and doping
concentrations.
(b) The base region must be very thin and lightly doped.
(c) The emitter junction is forward biased and collector junction is reverse
biased.
(d) Both the emitter junction as well as the collector junction are forward
biased.
Question 14.7 For a transistor amplifier, the voltage gain
(a) remains constant for all frequencies.
(b) is high at high and low frequencies and constant in the middle frequency
range.
(c) is low at high and low frequencies and constant at mid frequencies.
(d) None of the above.
Question 14.8 In half-wave rectification, what is the output
frequency if the input frequency is 50 Hz. What is the output frequency of a
full-wave rectifier for the same input frequency.
Question 14.9 For a CE-transistor amplifier, the audio signal
voltage across the collected resistance of 2 kΩ is 2 V. Suppose the current
amplification factor of the transistor is 100, find the input signal voltage and
base current, if the base resistance is 1 kΩ.
Question 14.10 Two amplifiers are connected one after the
other in series (cascaded). The first amplifier has a voltage gain of 10 and the
second has a voltage gain of 20. If the input signal is 0.01 volt, calculate the
output ac signal.
Question 14.11 A p-n photodiode is fabricated from a
semiconductor with band gap of 2.8 eV. Can it detect a wavelength of 6000 nm?
ADDITIONAL EXERCISES QUESTIONS
Question 14.12 The number of silicon atoms per m3 is 5 ×
1028. This is doped simultaneously with 5 × 1022 atoms per m3 of Arsenic and 5 ×
1020 per m3 atoms of Indium. Calculate the number of electrons and holes. Given
that ni = 1.5 × 1016 m–3. Is the material n-type or p-type?
Question 14.13 In an intrinsic semiconductor the energy gap
Eg is 1.2eV. Its hole mobility is much smaller than electron mobility and
independent of temperature. What is the ratio between conductivity at 600K and
that at 300K? Assume that the temperature dependence of intrinsic carrier
concentration ni is given by 0 exp – 2 g i B E n n k T = where n0 is a constant.
Question 14.14 In a p-n junction diode, the current I can
be expressed as 0 exp – 1 2 B eV I I k T where I0 is called the reverse
saturation current, V is the voltage across the diode and is positive for
forward bias and negative for reverse bias, and I is the current through the
diode, kB is the Boltzmann constant (8.6×10–5 eV/K) and T is the absolute
temperature. If for a given diode I0 = 5 × 10–12 A and T = 300 K, then (a) What
will be the forward current at a forward voltage of 0.6 V?
(b) What will be the increase in the current if the voltage
across the diode is increased to 0.7 V?
(c) What is the dynamic resistance?
(d) What will be the current if reverse bias voltage changes from 1 V to 2 V?
Question 14.15 You are given the two circuits as shown in
Fig.14.44. Show that circuit (a) acts as OR gate while the circuit (b) acts as
AND gate.
Question 14.16 Write the truth table for a NAND gate
connected as given in Fig. 14.45.Hence identify the exact logic operation
carried out by this circuit.
Question 14.17 You are given two circuits as shown in Fig.
14.46, which consist of NAND gates. Identify the logic operation carried out by
the two circuits.
Question 14.18 Write the truth table for circuit given in
Fig. 14.47 below consisting of NOR gates and identify the logic operation (OR,
AND, NOT) which this circuit is performing. (Hint: A = 0, B = 1 then A and B
inputs of second NOR gate will be 0 and hence Y=1. Similarly work out the values
of Y for other combinations of A and B. Compare with the truth table of OR, AND,
NOT gates and find the correct one.)
Question 14.19 Write the truth table for the circuits given
in Fig. 14.48 consisting of NOR gates only. Identify the logic operations (OR,
AND, NOT) performed by the two circuits.
:: Chapter 15 - Communication Systems ::
Question 15.1 Which of the following frequencies will be
suitable for beyond-thehorizon communication using sky waves? (a) 10 kHz (b) 10
MHz (c) 1 GHz (d) 1000 GHz
Question 15.2 Frequencies in the UHF range normally
propagate by means of:
(a) Ground waves.
(b) Sky waves.
(c) Surface waves.
(d) Space waves.
Question 15.3 Digital signals (i) do not provide a
continuous set of values, (ii) represent values as discrete steps, (iii) can
utilize binary system, and (iv) can utilize decimal as well as binary systems.
Which of the above statements are true?
(a) (i) and (ii) only
(b) (ii) and (iii) only
(c) (i), (ii) and (iii) but not (iv)
(d) All of (i), (ii), (iii) and (iv).
Question 15.4 Is it necessary for a transmitting antenna to
be at the same height as that of the receiving antenna for line-of-sight
communication? A TV transmitting antenna is 81m tall. How much service area can
it cover if the receiving antenna is at the ground level?
Question 15.5 A carrier wave of peak voltage 12V is used to
transmit a message signal. What should be the peak voltage of the modulating
signal in order to have a modulation index of 75%?
Question 15.6 A modulating signal is a square wave, as shown
in Fig. 15..14. The carrier wave is given by c (t ) = 2sin(8πt ) volts. (i)
Sketch the amplitude modulated waveform (ii) What is the modulation index?
Question 15.7 For an amplitude modulated wave, the maximum
amplitude is found to be 10V while the minimum amplitude is found to be 2V.
Determine the modulation index, μ. What would be the value of μ if the minimum
amplitude is zero volt?
Question 15.8 Due to economic reasons, only the upper
sideband of an AM wave is transmitted, but at the receiving station, there is a
facility for generating the carrier. Show that if a device is available which
can multiply two signals, then it is possible to recover the modulating signal
at the receiver station





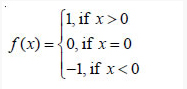
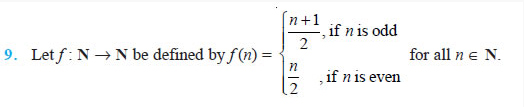


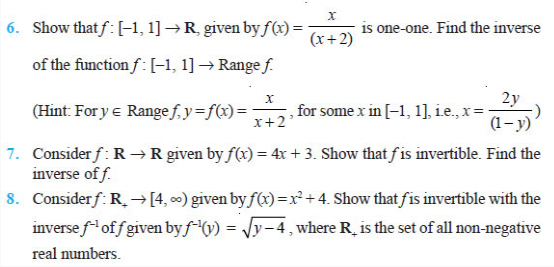
 EXERCISE
EXERCISE





 , write
, write
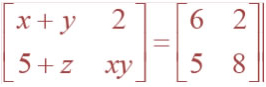
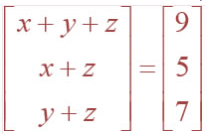
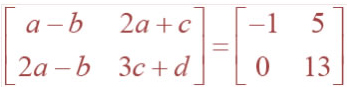
 .is a
square matrix, if
.is a
square matrix, if
 Find
each of the following:
Find
each of the following: Find
each of the following:
Find
each of the following: If ,
then compute (A+B) and (B – C). Also, verify that A + (B – C) = (A + B) – C.
If ,
then compute (A+B) and (B – C). Also, verify that A + (B – C) = (A + B) – C.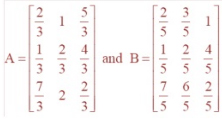 If ,
then compute 3A – 5B.
If ,
then compute 3A – 5B.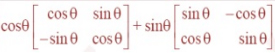
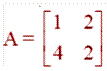 ,
then show that | 2A | = 4 | A |
,
then show that | 2A | = 4 | A |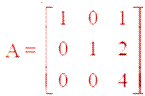 ,
then show that | 3 A | = 27 | A |
,
then show that | 3 A | = 27 | A | ,
find | A |
,
find | A |
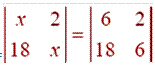 ,
then x is equal to
,
then x is equal to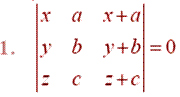
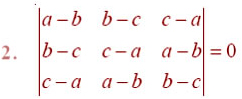
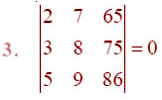
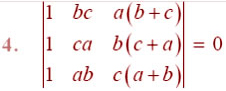
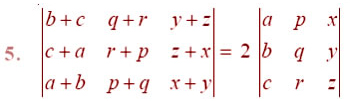
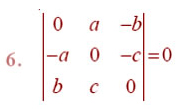
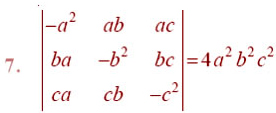
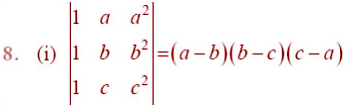
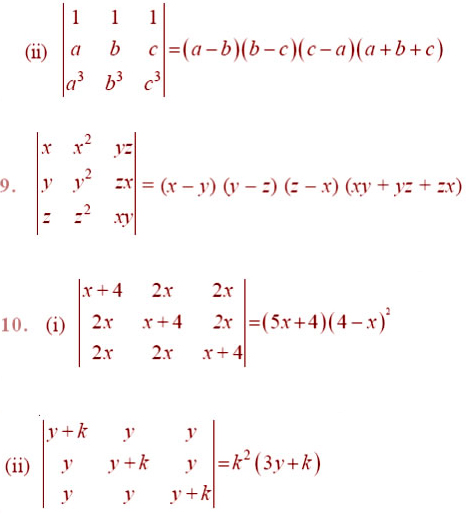
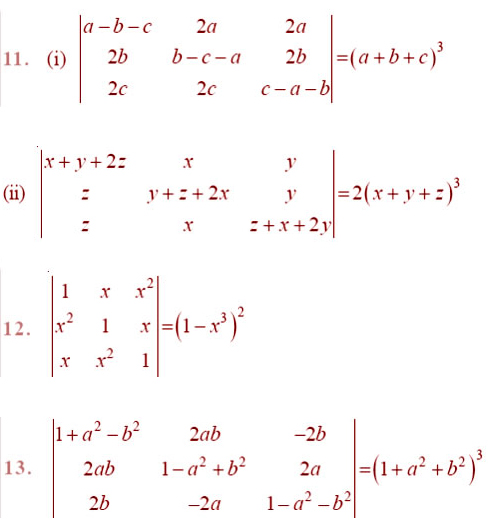
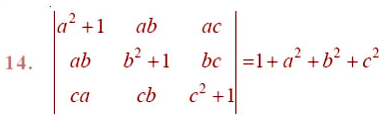

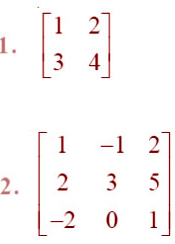
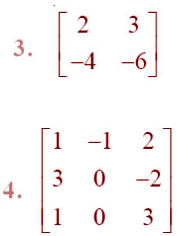
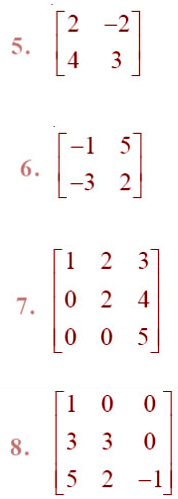


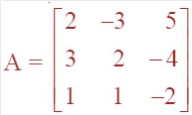 , find A–1. Using A–1 solve the system of equations 2x – 3y + 5z = 11 3x + 2y –
4z = – 5 x + y – 2z = – 3
, find A–1. Using A–1 solve the system of equations 2x – 3y + 5z = 11 3x + 2y –
4z = – 5 x + y – 2z = – 3